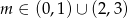/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 1048593

Wyznacz wszystkie wartości parametru 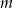m , dla których równanie

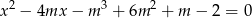
2 3 2 x − 4mx − m + 6m + m − 2 = 0

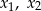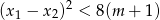ma dwa różne pierwiastki rzeczywiste x1, x2 takie, że 2 (x1 − x2) < 8(m + 1) .

Wersja PDF

Rozwiązanie

Sprawdźmy najpierw kiedy równanie ma dwa różne pierwiastki rzeczywiste.

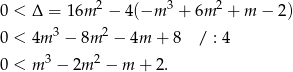
2 3 2 0 < Δ = 16m − 4(−m + 6m + m − 2) 0 < 4m 3 − 8m 2 − 4m + 8 / : 4 3 2 0 < m − 2m − m + 2.

Gołym okiem widać, że z prawej strony można wyłączyć 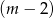(m − 2) przed nawias. Jeżeli jednak ktoś tego nie zauważył, to należy poszukać pierwiastków wymiernych wśród dzielników wyrazu wolnego, czyli wśród liczb -1,1,2,-2.

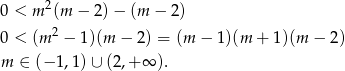
0 < m 2(m − 2) − (m − 2) 0 < (m 2 − 1)(m − 2) = (m − 1)(m + 1)(m − 2 ) m ∈ (− 1,1) ∪ (2,+ ∞ ).

Jeżeli równanie ma pierwiastki to możemy zapisać wzory Viète’a

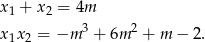
x + x = 4m 1 2 x1x2 = −m 3 + 6m 2 + m − 2.

Przekształćmy teraz warunek z treści zadania tak, aby móc zastosować wzory Viète’a.

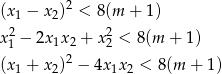
2 (x1 − x2) < 8(m + 1) x21 − 2x1x2 + x22 < 8 (m + 1) 2 (x1 + x2) − 4x1x2 < 8(m + 1)

Podstawiamy teraz ze wzorów Viète’a.

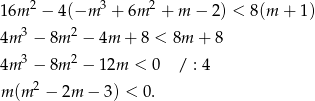
2 3 2 1 6m − 4(−m + 6m + m − 2) < 8(m + 1) 4m 3 − 8m 2 − 4m + 8 < 8m + 8 4m 3 − 8m 2 − 12m < 0 / : 4 2 m (m − 2m − 3) < 0.

Rozłóżmy teraz trójmian w nawiasie.

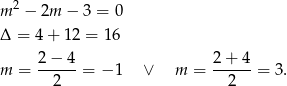
2 m − 2m − 3 = 0 Δ = 4 + 12 = 1 6 m = 2−-4-= − 1 ∨ m = 2-+-4-= 3. 2 2

Mamy więc nierówność

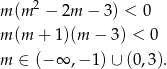
2 m (m − 2m − 3) < 0 m (m + 1)(m − 3) < 0 m ∈ (− ∞ ,− 1) ∪ (0,3).

Uwzględniając warunek z 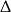Δ -ą mamy

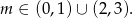
m ∈ (0,1)∪ (2,3 ).

 
Odpowiedź: m ∈ (0,1)∪ (2,3)

Wersja PDF