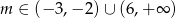/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 2920656

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich 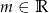m ∈ R równanie 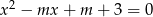2 x − mx + m + 3 = 0 ma dwa różne rozwiązania, których suma odwrotności jest mniejsza od 1?

Rozwiązanie

Najpierw sprawdźmy, kiedy równanie ma dwa różne rozwiązania

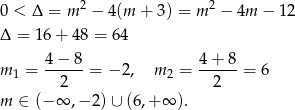
2 2 0 < Δ = m − 4 (m + 3) = m − 4m − 12 Δ = 16+ 48 = 64 4 − 8 4 + 8 m 1 = ------= − 2 , m 2 = ------= 6 2 2 m ∈ (− ∞ ,− 2) ∪ (6,+ ∞ ).

Teraz pozostało rozwiązać nierówność

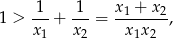
1 > 1-+ -1-= x1-+-x2, x1 x2 x 1x 2

ale zanim to zrobimy zapiszmy wzory Viète’a.

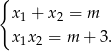
{ x1 + x2 = m x1x2 = m + 3.

Mamy więc

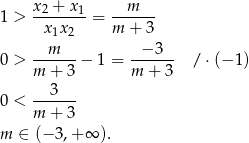
x 2 + x 1 m 1 > --------= ------ x1x2 m + 3 0 > --m--- − 1 = -−-3-- / ⋅(− 1) m + 3 m + 3 3 0 < ------ m + 3 m ∈ (−3 ,+∞ ).

W połączeniu z warunkiem na 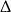Δ -ę otrzymujemy stąd

m ∈ (− 3,− 2) ∪ (6,+ ∞ ).

 
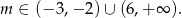
Odpowiedź: m ∈ (− 3,− 2)∪ (6 ,+∞ )

Wersja PDF