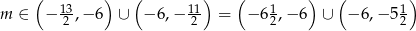/Szkoła średnia/Równania/Kwadratowe/Z parametrem

Zadanie nr 6007313

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 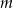m , dla których równanie

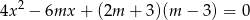
2 4x − 6mx + (2m + 3)(m − 3) = 0

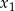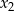ma dwa różne rozwiązania rzeczywiste x 1 i x2 , przy czym 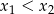x 1 < x2 , spełniające warunek

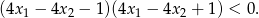
(4x 1 − 4x 2 − 1 )(4x 1 − 4x2 + 1) < 0.

Rozwiązanie

Sprawdźmy najpierw, kiedy równanie ma dwa różne rozwiązania rzeczywiste.

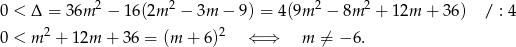
2 2 2 2 0 < Δ = 36m − 16(2m − 3m − 9 ) = 4(9m − 8m + 12m + 36 ) / : 4 0 < m 2 + 12m + 36 = (m + 6)2 ⇐ ⇒ m ⁄= − 6.

Sposób I

Jak zauważyliśmy powyżej, 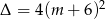2 Δ = 4(m + 6 ) , więc

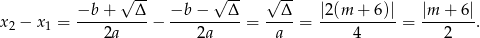
-- -- -- −b + √ Δ −b − √ Δ √ Δ |2(m + 6)| |m + 6| x2 − x1 = ----------− ---------- = ----= -----------= -------. 2a 2a a 4 2

Zauważmy teraz, że

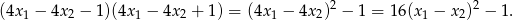
(4x1 − 4x2 − 1)(4x 1 − 4x 2 + 1 ) = (4x1 − 4x2)2 − 1 = 16 (x 1 − x 2)2 − 1 .

Pozostało więc rozwiązać nierówność

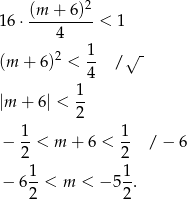
(m + 6)2 16 ⋅--------- < 1 4 2 1- √ - (m + 6) < 4 / 1 |m + 6 | < -- 2 − 1-< m + 6 < 1- / − 6 2 2 1- 1- − 62 < m < − 52.

uwzględniając warunek z 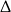Δ -ą mamy stąd

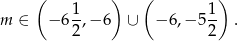
( ) ( ) 1- 1- m ∈ − 62 ,− 6 ∪ − 6,− 52 .

Sposób II

Przy założeniu 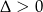Δ > 0 możemy zapisać wzory Viète’a.

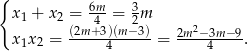
{ x1 + x2 = 6m4-= 32m (2m+-3)(m-−3) 2m2−-3m−9 x1x2 = 4 = 4 .

Zauważmy teraz, że

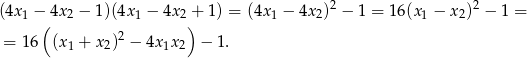
2 2 (4x1 −(4x2 − 1)(4x 1 − 4x 2 +) 1 ) = (4x1 − 4x2) − 1 = 16 (x1 − x 2) − 1 = = 16 (x + x )2 − 4x x − 1. 1 2 1 2

Pozostało więc rozwiązać nierówność

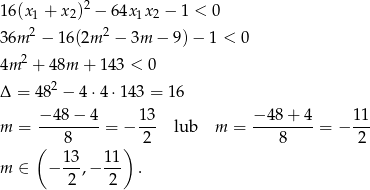
16(x1 + x2)2 − 64x1x2 − 1 < 0 2 2 36m − 1 6(2m − 3m − 9) − 1 < 0 4m 2 + 48m + 14 3 < 0 Δ = 4 82 − 4 ⋅4 ⋅143 = 16 − 48− 4 13 − 48 + 4 11 m = ---------= − --- lub m = ---------= − --- ( 8 ) 2 8 2 13- 11- m ∈ − 2 ,− 2 .

Uwzględniając warunek z 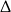Δ -ą mamy więc

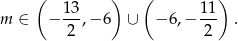
( ) ( ) 13- 11- m ∈ − 2 ,− 6 ∪ − 6,− 2 .

 
Odpowiedź: ( 13 ) ( 11) ( 1 ) ( 1) m ∈ − 2 ,− 6 ∪ −6 ,− 2 = − 62,− 6 ∪ − 6,− 5 2

Wersja PDF