Zadanie nr 2360976
Czworokąt 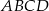 jest trapezem prostokątnym, w którym
jest trapezem prostokątnym, w którym 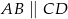 . Wykaż że
. Wykaż że
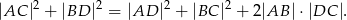
Rozwiązanie
Zaczynamy oczywiście od rysunku.
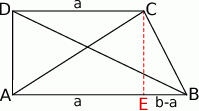
Przy oznaczeniach z rysunku, korzystając z twierdzeń Pitagorasa w trójkątach 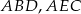 i
i 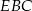 mamy
mamy
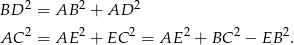
Stąd
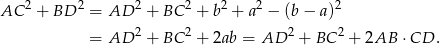
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
