Zadanie nr 8476138
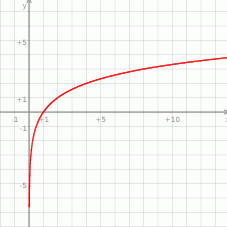
Na rysunku przedstawiony jest wykres funkcji logarytmicznej opisanej wzorem 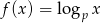 .
.
- Na podstawie tego wykresu wyznacz
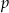 .
. - Oblicz
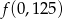 .
. - Sporządź wykres funkcji
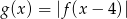 .
. - Podaj miejsce zerowe funkcji
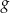 .
.
Rozwiązanie
Zadanie trochę ryzykowne, bo musi być dokładny rysunek.
- Jak się dokładnie przyjrzymy, to widać, że
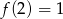 . To oznacza, że
. To oznacza, że 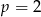 (bo
(bo 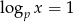 oznacza, że
oznacza, że 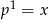 ).
).
Odpowiedź: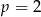
-
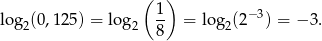
Odpowiedź: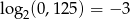
- Korzystamy ze wzoru na przesunięcie funkcji
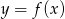 o wektor
o wektor ![→ v = [a,b]](https://img.zadania.info/zad/8476138/HzadR8x.gif) :
: 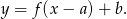
W naszej sytuacji, wykres funkcji
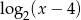 jest przesunięty o wektor
jest przesunięty o wektor ![[4,0 ]](https://img.zadania.info/zad/8476138/HzadR11x.gif) , czyli o 4 jednostki w prawo (niebieski wykres).
, czyli o 4 jednostki w prawo (niebieski wykres). 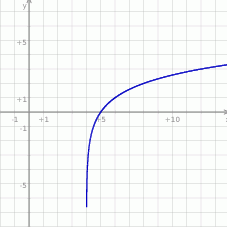
Aby otrzymać
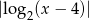 trzeba część która jest na dole ‘odbić’ do góry – zielony wykres.
trzeba część która jest na dole ‘odbić’ do góry – zielony wykres. 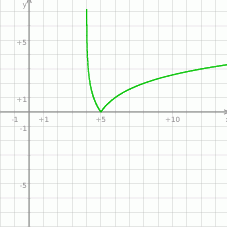
- Miejsce zerowe to oczywiście
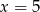 .
.
Odpowiedź: