/Szkoła średnia/Funkcje - wykresy/Logarytmy

Zadanie nr 9185924

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest wykres funkcji logarytmicznej 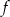f .

PIC

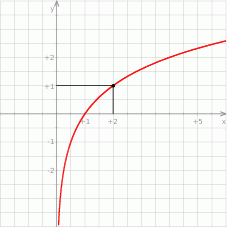
  • Wyznacz wzór funkcji f .
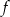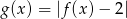  • Narysuj wykres funkcji g(x) = |f (x)− 2| .
  • Odczytaj z rysunku zbiór argumentów, dla których wartości funkcji 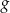g są nie mniejsze od wartości funkcji f .

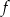Rozwiązanie

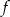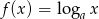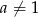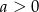  • Wiemy, że funkcja f jest postaci f(x ) = lo gax , gdzie a ⁄= 1 i a > 0 . Ponadto, z rysunku wiemy, że 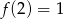f(2) = 1 . Mamy zatem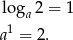
    lo ga2 = 1 1 a = 2.

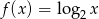    Zatem f(x) = log x 2 .  
    Odpowiedź: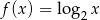 f(x) = lo g2x

  • Aby otrzymać wykres funkcji 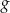g przesuwamy wykres funkcji o 2 jednostki w dół, a potem odbijamy część poniżej osi 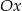Ox do góry.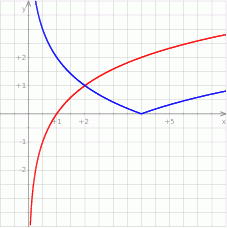
    PIC
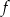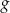  • Na początek upewnijmy się, że wykresy funkcji f i g przecinają się w punkcie 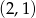(2,1) . Wiemy, wykres funkcji 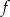f przechodzi przez ten punkt, ponadto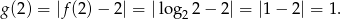
    g (2) = |f(2)− 2| = |log22 − 2 | = |1 − 2| = 1.

    Zatem wykres funkcji 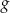g też przechodzi przez ten punkt. Widać zatem, że 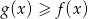g(x) ≥ f (x) dla x ∈ (0 ,2⟩ .  
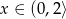    Odpowiedź: x ∈ (0,2⟩

Wersja PDF