Zadanie nr 2301192
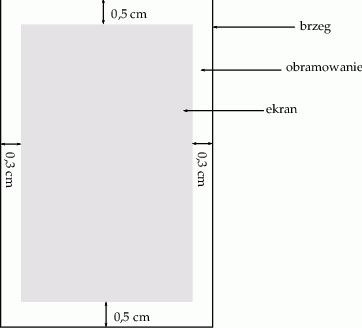
Należy zaprojektować wymiary prostokątnego ekranu smartfona, tak aby odległości tego ekranu od krótszych brzegów smartfona były równe 0,5 cm każda, a odległości tego ekranu od dłuższych brzegów smartfona były równe 0,3 cm każda (zobacz rysunek – ekran zaznaczono kolorem szarym). Sam ekran ma mieć powierzchnię 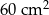 . Wyznacz takie wymiary ekranu smartfona, przy których powierzchnia ekranu wraz z obramowaniem jest najmniejsza.
. Wyznacz takie wymiary ekranu smartfona, przy których powierzchnia ekranu wraz z obramowaniem jest najmniejsza.
Rozwiązanie
Oznaczmy przez  długość krótszego boku ekranu smartfona. Wtedy dłuższy bok tego ekranu ma długość
długość krótszego boku ekranu smartfona. Wtedy dłuższy bok tego ekranu ma długość 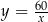 . Musimy teraz znaleźć najmniejszą wartość funkcji
. Musimy teraz znaleźć najmniejszą wartość funkcji
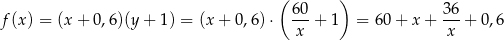
określonej dla 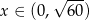 (bo
(bo  ma być krótszym bokiem ekranu). Liczymy pochodną
ma być krótszym bokiem ekranu). Liczymy pochodną
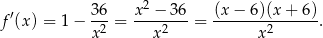
Widać teraz, że pochodna jest ujemna w przedziale 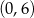 i dodatnia w przedziale
i dodatnia w przedziale 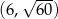 . To oznacza, że funkcja
. To oznacza, że funkcja 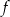 maleje w przedziale
maleje w przedziale 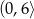 i rośnie w przedziale
i rośnie w przedziale 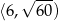 . W takim razie najmniejsze pole otrzymamy dla
. W takim razie najmniejsze pole otrzymamy dla 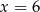 . Dłuższy bok ekranu ma wtedy długość
. Dłuższy bok ekranu ma wtedy długość
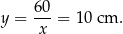
Odpowiedź: 6 cm i 10 cm.

