/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema/Najmniejsze pole

Zadanie nr 6792762

Na kole o promieniu 1 opisano trójkąt prostokątny. Oblicz długości boków tego trójkąta, którego pole jest najmniejsze.

Wersja PDF

Rozwiązanie

Szkicujemy trójkąt prostokątny – oznaczmy 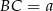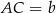BC = a , AC = b i AB = c .

PIC

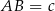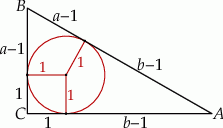
Z rysunku powinno być jasne, że

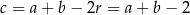
c = a + b− 2r = a + b − 2

(mogliśmy też skorzystać ze wzoru 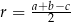a+b −c r = --2--- na promień okręgu wpisanego w trójkąt prostokątny). Mamy zatem

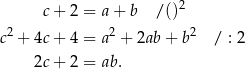
c+ 2 = a + b / ()2 2 2 2 c + 4c+ 4 = a + 2ab + b / : 2 2c+ 2 = ab.

Podstawiamy w tej równości 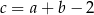c = a+ b− 2 i obliczamy 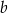b w zależności od a .

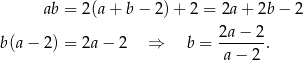
ab = 2 (a+ b − 2) + 2 = 2a+ 2b− 2 b(a − 2) = 2a − 2 ⇒ b = 2a-−-2-. a− 2

Pozostało wyznaczyć najmniejszą wartość funkcji

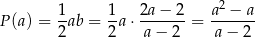
2 P (a) = 1-ab = 1-a⋅ 2a−--2-= a--−-a 2 2 a − 2 a− 2

określoną dla 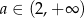a ∈ (2,+ ∞ ) . Liczymy pochodną

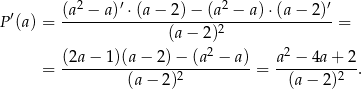
′ (a2 −-a-)′ ⋅(a−-2)−-(a2 −-a)-⋅(a-−-2)′- P (a) = (a − 2)2 = 2 2 = (2a−--1)(a−--2)−--(a-−-a)-= a--−-4a-+-2. (a− 2 )2 (a− 2)2

Rozkładamy trójmian w liczniku.

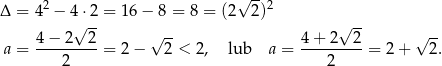
√ -- Δ = 42 − 4 ⋅2 = 16 − 8 = 8 = (2 2)2 √ -- √ -- √ -- √ -- a = 4−-2---2-= 2 − 2 < 2, lub a = 4-+-2--2-= 2+ 2. 2 2

Mamy zatem

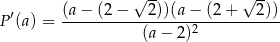
√ -- √ -- (a − (2 − 2))(a − (2 + 2)) P′(a) = ------------------2----------- (a − 2)

i widzimy, że pochodna jest ujemna dla 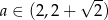√ -- a ∈ (2 ,2+ 2) i dodatnia dla 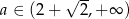√ -- a ∈ (2 + 2,+ ∞ ) . W takim razie funkcja 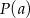P(a) maleje w przedziale 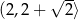√ -- (2,2 + 2⟩ i rośnie w przedziale 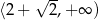√ -- ⟨2 + 2,+ ∞ ) . Najmniejszą wartość pola otrzymamy więc dla 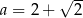√ -- a = 2+ 2 . Mamy wtedy

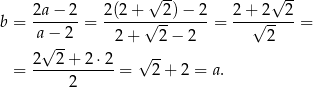
√ -- √ -- b = 2a-−-2-= 2(2+-√--2)−--2-= 2+√2---2-= a − 2 2 + 2 − 2 2 2√ 2-+ 2 ⋅2 √ -- = ------------= 2 + 2 = a. 2

i

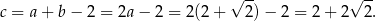
√ -- √ -- c = a + b − 2 = 2a − 2 = 2(2+ 2)− 2 = 2 + 2 2.

 
Odpowiedź: √ -- √ -- √ -- 2 + 2, 2+ 2, 2 + 2 2

Wersja PDF