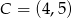/Szkoła średnia/Geometria/Geometria analityczna/Zadania na ekstremum

Zadanie nr 1673841

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane są punkty 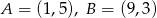A = (1,5), B = (9,3) i prosta 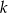k o równaniu 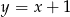y = x+ 1 . Oblicz współrzędne punktu 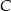C leżącego na prostej 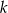k , dla którego suma 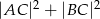|AC |2 + |BC |2 jest najmniejsza.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

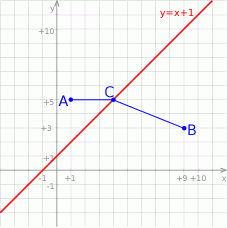
Skoro punkt 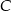C leży na prostej o równaniu 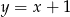y = x+ 1 to ma współrzędne postaci 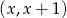(x,x + 1) . Mamy zatem

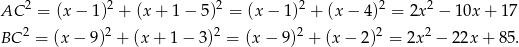
AC 2 = (x − 1)2 + (x + 1 − 5)2 = (x − 1)2 + (x − 4)2 = 2x 2 − 10x + 17 2 2 2 2 2 2 BC = (x− 9) + (x+ 1− 3) = (x − 9) + (x− 2) = 2x − 22x + 85.

Stąd

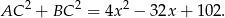
AC 2 + BC 2 = 4x2 − 32x + 1 02.

Wykresem otrzymanej funkcji kwadratowej jest parabola o ramionach skierowanych w górę, więc najmniejszą wartość otrzymamy w wierzchołku, czyli dla

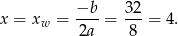
−b 32 x = xw = ----= ---= 4. 2a 8

Wtedy 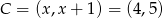C = (x,x + 1) = (4 ,5) .  
Odpowiedź: C = (4,5)

Wersja PDF