Zadanie nr 6217131
Wykaż, że jeśli 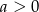 , to
, to 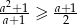 .
.
Rozwiązanie
Przekształcamy podaną nierówność
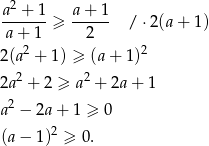
Otrzymana nierówność jest oczywiście prawdziwa, a przekształcenia były równoważnościami, więc wyjściowa nierówność również musiała być prawdziwa.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeśli 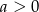 , to
, to 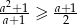 .
.
Przekształcamy podaną nierówność
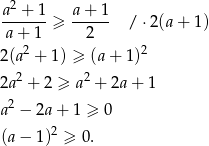
Otrzymana nierówność jest oczywiście prawdziwa, a przekształcenia były równoważnościami, więc wyjściowa nierówność również musiała być prawdziwa.
