/Szkoła średnia/Nierówności/Udowodnij.../Wymierne

Zadanie nr 9014262

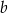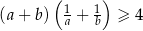Wykaż, że jeżeli a i b są liczbami rzeczywistymi dodatnimi, to ( ) (a + b) 1 + 1 ≥ 4 a b .

Wersja PDF

Rozwiązanie

Przekształcamy daną nierówność w sposób równoważny – liczby 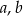a,b są dodatnie, więc możemy przez nie mnożyć nierówność stronami.

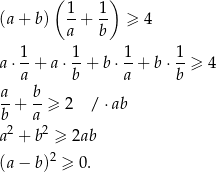
( ) (a + b) 1-+ 1- ≥ 4 a b 1 1 1 1 a ⋅--+ a ⋅--+ b ⋅--+ b ⋅--≥ 4 a b a b a-+ b-≥ 2 / ⋅ ab b a a2 + b2 ≥ 2ab (a − b)2 ≥ 0.

Otrzymana nierówność jest oczywiście spełniona.

Wersja PDF