/Szkoła średnia/Zadania z treścią/Geometryczne

Zadanie nr 9385385

Dane są dwie prostokątne działki. Działka pierwsza ma powierzchnię równą 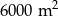60 00 m 2 . Działka druga ma wymiary większe od wymiarów pierwszej działki o 10 m i 15 m oraz powierzchnię większą o 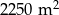2250 m 2 . Oblicz wymiary pierwszej działki.

Wersja PDF

Rozwiązanie

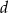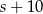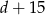Oznaczmy szerokość i długość pierwszej działki przez s i d . W takim razie druga działka ma wymiary s+ 10 i d + 15 i otrzymujemy układ równań

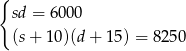
{ sd = 600 0 (s+ 10)(d+ 15) = 82 50

Przekształćmy drugie równanie korzystając z równości 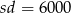sd = 6000 .

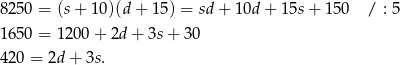
8250 = (s + 10)(d + 1 5) = sd+ 10d + 15s + 150 / : 5 1650 = 1 200+ 2d + 3s+ 30 420 = 2d + 3s.

Podstawiamy teraz do tej równości 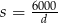6000 s = d .

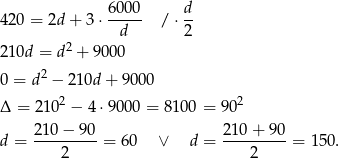
6 000 d 420 = 2d + 3 ⋅----- /⋅ -- d 2 210d = d2 + 9000 2 0 = d − 210d + 9 000 Δ = 2102 − 4⋅9 000 = 810 0 = 902 d = 21-0−--90 = 60 ∨ d = 21-0+-9-0 = 150 . 2 2

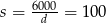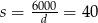Wtedy 6000 s = -d--= 10 0 i 6000 s = -d--= 40 . Zatem pierwsza działka ma wymiary 60 m na 100 m lub 150 m na 40 m.  
Odpowiedź: 60 m na 100 m lub 150 m na 40 m

Wersja PDF