Zadanie nr 7984285
Do kina wybrało się 7 osób, wśród nich Basia i Janek. Wszyscy usiedli w jednym rzędzie, w którym jest dokładnie 7 wolnych miejsc. Oblicz, na ile sposobów wymienione osoby mogą zająć miejsca tak, by Basia i Janek siedzieli obok siebie. Oblicz też prawdopodobieństwo tego, że przy losowym zajmowaniu miejsc Basia i Janek nie siedzą obok siebie.
Rozwiązanie
Dwa sąsiednie miejsca, na których usiądą Basia i Janek możemy wybrać na 6 sposobów. Jeżeli te miejsca są ustalone, to Basię i Janka możemy posadzić na dwa sposoby, a pozostałe osoby zupełnie dowolnie, czyli na 5! sposobów. W sumie jest więc
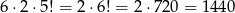
możliwości.
Siedem osób może usiąść na 7 miejscach na
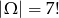
sposobów, więc prawdopodobieństwo zdarzenia przeciwnego jest równe
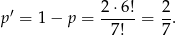
Zatem
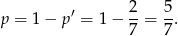
Odpowiedź: Na 1440 sposobów, 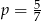 .
.

