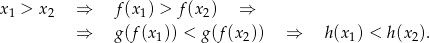Zadanie nr 6187487
Uzasadnij, że złożenie funkcji rosnącej i malejącej jest funkcją malejącą.
Rozwiązanie
Oznaczmy podane funkcje przez 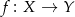 i
i 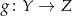 , wtedy ich złożenie to funkcja
, wtedy ich złożenie to funkcja 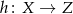 dana wzorem
dana wzorem
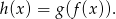
Wiemy, że
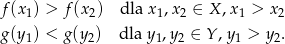
A chcemy udowodnić, że
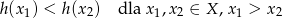
Liczymy
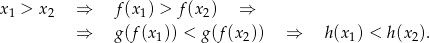
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Uzasadnij, że złożenie funkcji rosnącej i malejącej jest funkcją malejącą.
Oznaczmy podane funkcje przez 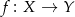 i
i 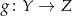 , wtedy ich złożenie to funkcja
, wtedy ich złożenie to funkcja 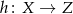 dana wzorem
dana wzorem
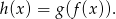
Wiemy, że
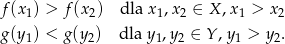
A chcemy udowodnić, że
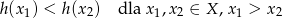
Liczymy