/Szkoła średnia/Równania/Potęgowe i pierwiastki

Zadanie nr 8974778

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 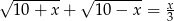√ ------- √ ------- x 10 + x + 10 − x = 3 .

Rozwiązanie

Wyrażenia pod pierwiastkami muszą być nieujemne, czyli

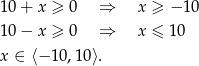
10 + x ≥ 0 ⇒ x ≥ − 10 10 − x ≥ 0 ⇒ x ≤ 1 0 x ∈ ⟨− 1 0,10⟩.

Chcielibyśmy teraz podnieść równanie stronami do kwadratu. Na ogół prowadzi to do większej ilości rozwiązań (np. podnosząc 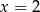x = 2 do kwadatu dostajemy ’fałszywe’ rozwiązanie 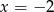x = − 2 ), więc musimy pamiętać o tym, żeby na koniec sprawdzić otrzymane rozwiązania. Inny sposób, to założyć, że obie strony są nieujemne, czyli, że 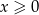x ≥ 0 , wtedy nie musimy sprawdzać otrzymanych rozwiązań. My postąpimy tą drugą metodą.

Podnosimy równanie do kwadratu.

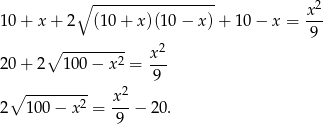
∘ ----------------- 2 x-- 10 + x + 2 (1 0+ x)(10− x) + 10 − x = 9 ∘ --------- x 2 20 + 2 1 00− x2 = --- 9 ∘ --------2 x2- 2 10 0− x = 9 − 2 0.

Chcemy ponownie podnieść do kwadratu, sprawdźmy jednak najpierw kiedy prawa strona jest nieujemna

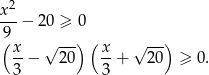
x2 ---− 20 ≥ 0 9( √ --) ( √ --) x− 20 x-+ 20 ≥ 0. 3 3

Ponieważ 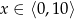x ∈ ⟨0 ,10⟩ , pierwszy nawias jest ujemny, a drugi dodatni. Oznacza to, że prawa strona ostatniego równania jest zawsze ujemna, czyli równanie jest sprzeczne.  
Odpowiedź: Równanie sprzeczne.

Wersja PDF
Rozwiązanie Losuj ponownie