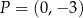/Szkoła średnia/Funkcje - wykresy/Liniowy/Różne

Zadanie nr 5806125

Dodaj do ulubionych
Dodaj do rozwiązanych

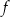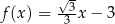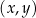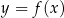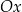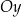Funkcja liniowa f jest określona wzorem √-3 f (x) = 3 x − 3 . W kartezjańskim układzie współrzędnych (x,y) wykres funkcji y = f(x) jest prostą nachyloną do osi Ox pod kątem ostrym α i przecina oś Oy w punkcie 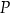P . Oblicz sinα oraz współrzędne punktu P .

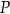Rozwiązanie

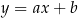Współczynnik kierunkowy a we wzorze y = ax + b funkcji liniowej jest równy tangensowi kąta α nachylenia wykresu tej funkcji do osi Ox

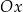
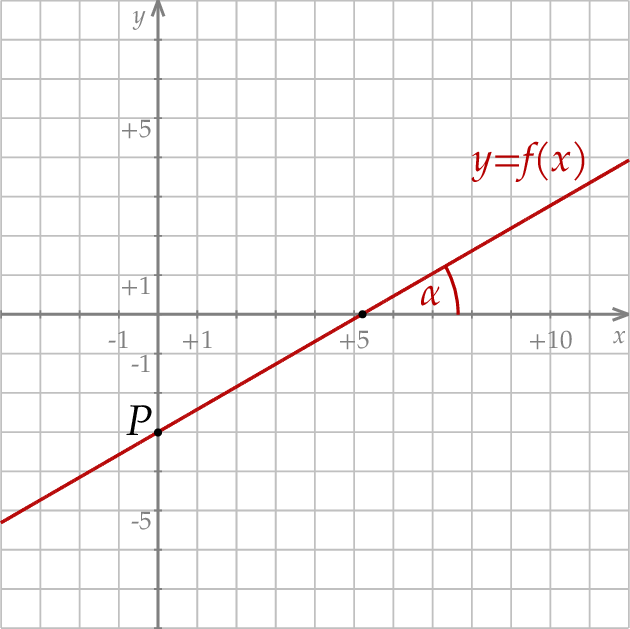
ZINFO-FIGURE

Mamy zatem

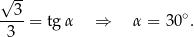
√ -- --3- ∘ 3 = tg α ⇒ α = 30 .

Stąd

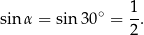
∘ 1- sinα = sin 30 = 2.

Współrzędne punktu 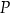P to

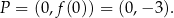
P = (0,f(0)) = (0,− 3).

 
Odpowiedź: 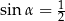sin α = 12 , P = (0,− 3)

Wersja PDF
Rozwiązanie Losuj ponownie