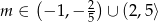/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Nierówności z pierwiastkami

Zadanie nr 5842259

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 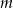m , dla których równanie 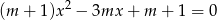(m + 1)x2 − 3mx + m + 1 = 0 ma dwa różne pierwiastki takie, że ich suma jest nie większa niż 2,5.

Rozwiązanie

Sprawdźmy najpierw kiedy równanie ma dwa pierwiastki. Oczywiście musi być kwadratowe, czyli 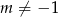m ⁄= − 1 oraz

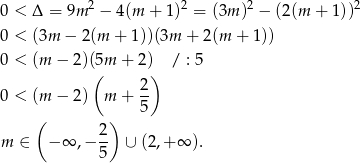
2 2 2 2 0 < Δ = 9m − 4(m + 1) = (3m ) − (2(m + 1)) 0 < (3m − 2 (m + 1))(3m + 2(m + 1)) 0 < (m − 2)(5(m + 2)) / : 5 2 0 < (m − 2) m + -- ( ) 5 2- m ∈ − ∞ ,− 5 ∪ (2 ,+∞ ).

Na mocy wzorów Viète’a mamy

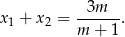
-3m--- x 1 + x 2 = m + 1.

Musimy więc rozwiązać nierówność

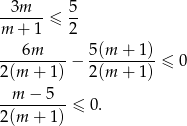
--3m-- ≤ 5- m + 1 2 6m 5 (m + 1) --------- − --------- ≤ 0 2(m + 1) 2 (m + 1) --m-−--5- 2(m + 1) ≤ 0.

Ponieważ iloraz dwóch liczb jest ujemny dokładnie wtedy, gdy ich iloczyn jest ujemny, powyższa nierówność jest równoważna nierówności kwadratowej

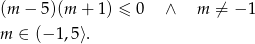
(m − 5)(m + 1) ≤ 0 ∧ m ⁄= − 1 m ∈ (− 1,5⟩.

W połączeniu z warunkiem na 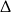Δ -ę mamy więc

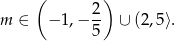
( 2) m ∈ − 1,− -- ∪ (2,5⟩. 5

 
Odpowiedź: ( ) m ∈ − 1,− 25 ∪ (2,5⟩

Wersja PDF