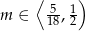/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Nierówności z pierwiastkami

Zadanie nr 8061381

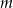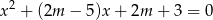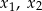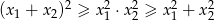Wyznacz wszystkie wartości parametru m , dla których równanie x 2 + (2m − 5)x + 2m + 3 = 0 ma dwa różne pierwiastki rzeczywiste x1, x 2 takie, że (x1 + x2)2 ≥ x 21 ⋅x22 ≥ x21 + x22 .

Wersja PDF

Rozwiązanie

Sprawdzamy najpierw, kiedy równanie ma dwa różne pierwiastki.

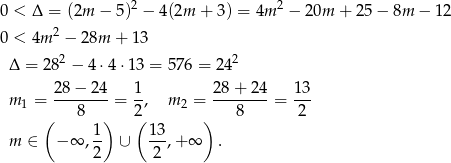
2 2 0 < Δ = (2m − 5) − 4(2m + 3) = 4m − 20m + 25− 8m − 12 0 < 4m 2 − 28m + 13 2 2 Δ = 28 − 4 ⋅4⋅ 13 = 576 = 24 2 8− 24 1 28 + 24 13 m 1 = -------- = --, m 2 = --------= --- ( 8 ) 2( ) 8 2 m ∈ − ∞ , 1 ∪ 1-3,+ ∞ . 2 2

Zapiszmy teraz wzory Viéte’a dla danego równania.

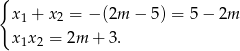
{ x1 + x2 = −(2m − 5) = 5− 2m x1x 2 = 2m + 3.

Musimy zatem rozwiązać nierówność

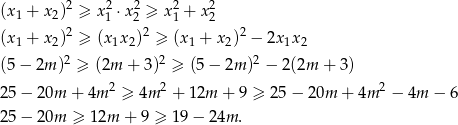
(x1 + x2)2 ≥ x21 ⋅x22 ≥ x21 + x22 2 2 2 (x1 + x2) ≥ (x1x2) ≥ (x 1 + x2) − 2x 1x2 (5− 2m )2 ≥ (2m + 3 )2 ≥ (5− 2m )2 − 2(2m + 3) 25− 20m + 4m 2 ≥ 4m 2 + 1 2m + 9 ≥ 25− 20m + 4m 2 − 4m − 6 25− 20m ≥ 12m + 9 ≥ 19 − 24m .

Zamieniamy teraz powyższą nierówność podwójną na układ dwóch nierówności.

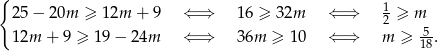
{ 25− 20m ≥ 12m + 9 ⇐ ⇒ 1 6 ≥ 32m ⇐ ⇒ 1 ≥ m 2 12m + 9 ≥ 19 − 24m ⇐ ⇒ 3 6m ≥ 10 ⇐ ⇒ m ≥ 158.

Bierzemy teraz część wspólną otrzymanego przedziału 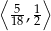⟨ 5- 1⟩ 18,2 z otrzymanym wcześniej zbiorem rozwiązań nierówności 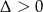Δ > 0 . Mamy zatem

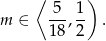
⟨ ) -5- 1- m ∈ 1 8,2 .

 
Odpowiedź: ⟨ 5- 1) m ∈ 18 ,2

Wersja PDF