Zadanie nr 3923924
Wyznacz wszystkie wartości parametru 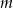 , dla których równanie
, dla których równanie 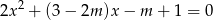 ma dwa różne pierwiastki
ma dwa różne pierwiastki 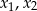 takie, że
takie, że 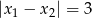 .
.
Rozwiązanie
Sprawdźmy najpierw, kiedy równanie ma dwa różne pierwiastki.
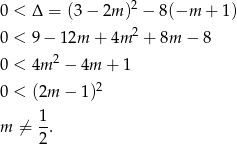
Sposób I
Przy założeniu 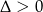 możemy skorzystać ze wzorów na pierwiastki.
możemy skorzystać ze wzorów na pierwiastki.
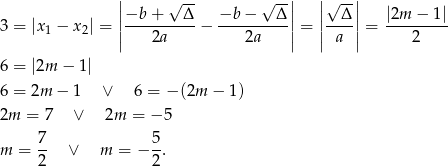
Sposób II
Przy założeniu 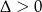 równanie ma dwa pierwiastki
równanie ma dwa pierwiastki 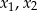 i możemy zastosować wzory Viète’a
i możemy zastosować wzory Viète’a
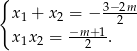
Przekształcamy teraz żądaną równość tak, aby móc zastosować wzory Viète’a.
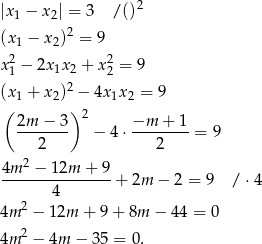
Rozwiązujemy otrzymane równanie kwadratowe
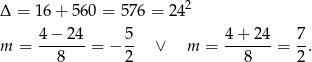
Odpowiedź: 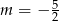 lub
lub