Zadanie nr 6285915
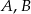 są zdarzeniami losowymi zawartymi w
są zdarzeniami losowymi zawartymi w 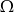 . Wykaż, że jeżeli
. Wykaż, że jeżeli 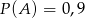 i
i 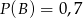 , to
, to 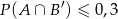 (
(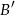 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 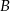 ).
).
Rozwiązanie
Sposób I
Rozpoczynamy od naszkicowania diagramu Venna.
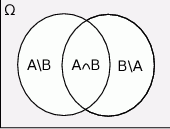
Przyglądając się diagramowi możemy zauważyć, że
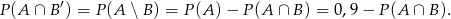
Musimy więc oszacować 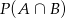 . Korzystamy z niezastąpionego wzoru na sumę zdarzeń
. Korzystamy z niezastąpionego wzoru na sumę zdarzeń
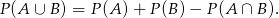
W szczególności
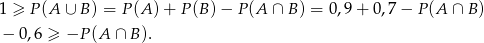
Mamy stąd
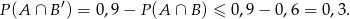
Sposób II
Zauważmy, że
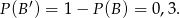
W takim razie
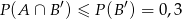
(bo 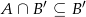 ).
).

