/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Własności cyfr

Zadanie nr 1682572

Dodaj do ulubionych
Dodaj do rozwiązanych

Z liczb ośmioelementowego zbioru 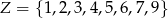Z = { 1,2,3,4,5,6,7,9 } tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.

Rozwiązanie

Wszystkich możliwości ustawienia danych 8 liczb jest

|Ω | = 8!

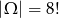
Sposób I

Każdy ciąg spełniający warunki zdania musi mieć jedną z postaci:

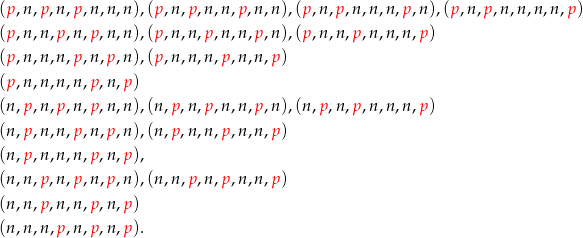
(p,n,p ,n,p,n ,n ,n),(p,n ,p,n,n,p ,n,n),(p ,n ,p,n,n ,n,p,n),(p ,n,p,n ,n,n,n,p ) (p,n,n ,p,n,p ,n ,n),(p,n ,n,p,n,n ,p,n),(p ,n ,n,p,n ,n,n,p) (p,n,n ,n,p,n ,p ,n),(p,n ,n,n,p,n ,n,p) (p,n,n ,n,n,p ,n ,p) (n,p,n ,p,n,p ,n ,n),(n,p ,n,p,n,n ,p,n),(n ,p ,n,p,n ,n,n,p) (n,p,n ,n,p,n ,p ,n),(n,p ,n,n,p,n ,n,p) (n,p,n ,n,n,p ,n ,p), (n,n,p ,n,p,n ,p ,n),(n,n ,p,n,p,n ,n,p) (n,n,p ,n,n,p ,n ,p) (n,n,n ,p,n,p ,n ,p).

W każdej z tych 20 konfiguracji liczby parzyste możemy wybrać na 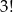3! sposobów, a liczby nieparzyste na 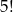5! sposobów. Interesujące nas prawdopodobieństwo jest więc równe

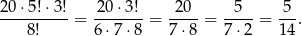
2 0⋅5 !⋅3! 20⋅ 3! 20 5 5 ---------- = ------- = ----= ---- = --. 8! 6 ⋅7 ⋅8 7⋅8 7 ⋅2 14

Sposób II

Tym razem spróbujmy wypisać złe konfiguracje. Jest 6 konfiguracji:

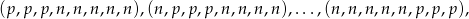
(p,p,p ,n,n,n ,n,n),(n,p ,p,p,n,n ,n,n),...,(n ,n,n,n,n ,p,p,p ),

w których wszystkie 3 liczb parzyste są obok siebie. Wypiszemy teraz liczbę konfiguracji, w których dwie liczby parzyste są obok siebie, a trzecia nie jest ich sąsiadem:

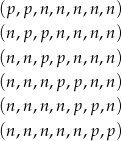
(p ,p,n,n ,n,n,n) (n ,p,p,n ,n,n,n) (n ,n,p,p ,n,n,n) (n ,n,n,p ,p,n,n) (n ,n,n,n ,p,p,n) (n ,n,n,n ,n,p,p)

Łatwo sprawdzić, że w każdym z 6 powyższych przypadków jest 5 sposobów dopisania brakującej 3 liczby parzystej tak, aby nie była sąsiadem dwóch sąsiednich liczb parzystych. W sumie jest więc

6 ⋅5 = 30

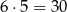
takich konfiguracji. W każdym z 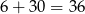6 + 30 = 36 przypadków liczby parzyste możemy wybrać na 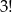3! sposobów, a liczby nieparzyste na 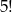5! sposobów. Interesujące nas prawdopodobieństwo jest więc równe

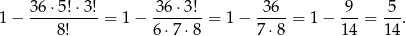
36-⋅5!-⋅3! -36⋅3-! -36- 9-- 5-- 1 − 8! = 1− 6 ⋅7⋅ 8 = 1 − 7 ⋅8 = 1− 14 = 14.

 
Odpowiedź: -5 14

Wersja PDF