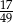/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Podzielność

Zadanie nr 9931722

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru liczb 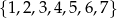{1,2,3 ,4 ,5,6,7} losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 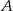A , polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 6.

Rozwiązanie

Za zdarzenia elementarne przyjmijmy pary wylosowanych liczb. Mamy zatem

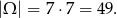
|Ω | = 7 ⋅7 = 49 .

Sposób I

Wypiszmy zdarzenia sprzyjające.

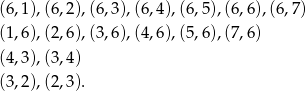
(6,1),(6,2),(6,3),(6,4 ),(6 ,5),(6,6),(6,7) (1,6),(2,6),(3,6),(4,6 ),(5 ,6),(7,6) (4,3),(3,4) (3,2),(2,3).

Prawdopodobieństwo jest więc równe 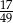1479 .

Sposób II

Jest jedno zdarzenie sprzyjające z dwoma równymi liczbami: 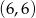(6,6) .

Obliczmy ile jest zdarzeń, gdy wybieramy dwie różne liczby. Jedną z wybranych liczb musi być 6 lub 3. Jeżeli wybieramy 6, to drugą liczbę możemy wybrać dowolnie, ale nie może być 6 (bo parę 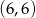(6,6) już liczyliśmy). Do tego możemy na dwa sposoby ustalić kolejność liczb. Jest więc

6 ⋅2 = 12

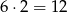
zdarzeń z 6-ką. Jeżeli jedną z liczb 3, to druga musi być parzysta i nie może być 6 (bo takie zdarzenia już liczyliśmy). Do tego ustalamy kolejność na dwa sposoby. Są więc

2⋅ 2 = 4

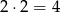
dodatkowe zdarzenia z 3-ką. W sumie jest więc

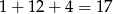
1 + 12 + 4 = 1 7

zdarzeń sprzyjających i prawdopodobieństwo wynosi 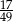17 49 .  
Odpowiedź: 17 49

Wersja PDF