Zadanie nr 1584155
Dane są dwa podzbiory zbioru liczb całkowitych:
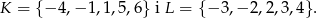
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni.
Rozwiązanie
Każdą z liczb możemy wybrać na 5 sposobów, więc
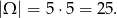
W zdarzeniach sprzyjających obie liczby muszą być tego samego znaku, tzn. albo obie są ujemne, albo obie są dodatnie. Dwie liczby ujemne możemy wybrać na
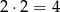
sposoby (każdą z liczb na dwa sposoby), a dwie dodatnie na
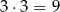
sposobów. Interesujące nas prawdopodobieństwo jest więc równe
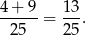
Odpowiedź: