/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Parzystość

Zadanie nr 4979694

Liczby 1, 2, 3, 4, 5, 6, 7, 8 ustawiamy losowo w szeregu. Oblicz prawdopodobieństwo, że w tym ustawieniu suma każdych dwóch sąsiednich liczb będzie nieparzysta. Wynik podaj w postaci ułamka nieskracalnego.

Wersja PDF

Rozwiązanie

Wszystkich możliwych ustawień 8 liczb jest

|Ω | = 8!.

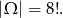
W zdarzeniach sprzyjających na przemian muszą stać liczby parzyste i liczby nieparzyste.

Sposób I

Policzmy takie zdarzenia. Pierwszą liczbę wybieramy dowolnie – na 8 możliwych sposobów. Drugą możemy już wybrać tylko na 4 sposoby, bo musi mieć inną parzystość niż pierwsza. Trzecią możemy wybrać na 3 sposoby – musi tej samej parzystości co pierwsza i musi być od niej różna. Czwartą możemy wybrać też 3 sposoby – musi mieć taką samą parzystość jak druga i być od niej różna. Analogicznie piątą i szóstą liczbę możemy wybrać na 2 sposoby, a przy wyborze liczb siódmej i ósmej nie mamy już żadnego wyboru. Zatem jest

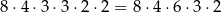
8⋅ 4⋅3 ⋅3 ⋅2⋅ 2 = 8 ⋅4⋅6 ⋅3 ⋅2

zdarzeń sprzyjających i prawdopodobieństwo wynosi

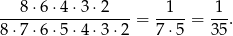
---8⋅-6⋅4-⋅3-⋅2--- = --1- = -1. 8 ⋅7⋅ 6⋅5 ⋅4 ⋅3⋅ 2 7 ⋅5 35

Sposób II

Tym razem zdarzenia sprzyjające policzmy odrobinę inaczej. Ile jest zdarzeń sprzyjających, w których pierwsza liczba jest parzysta? – jest ich 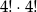4 !⋅4! , bo musimy mieć na przemian liczby parzyste i nieparzyste, oraz każdy z tych zbiorów może być dowolnie spermutowany. Dokładnie tyle samo jest układów z pierwszą liczbą nieparzystą. Zatem łącznie jest

2 ⋅4!⋅4!

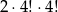
zdarzeń sprzyjających.

Prawdopodobieństwo liczymy tak samo jak w poprzednim sposobie.  
Odpowiedź: -1 35

Wersja PDF