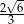/Szkoła średnia/Geometria/Stereometria/Zadania na ekstrema/Najmniejsza długość

Zadanie nr 7929840

Suma długości wysokości i długości jednej krawędzi podstawy graniastosłupa prawidłowego czworokątnego jest równa 2. Jaką najmniejszą długość może mieć przekątna takiego graniastosłupa.

Rozwiązanie

Zaczynamy od rysunku.

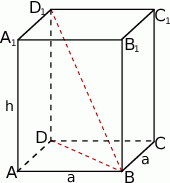
Wiemy, że 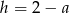h = 2 − a . Wyliczmy długość przekątnej.

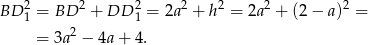
2 2 2 2 2 2 2 BD 1 = BD + DD 1 = 2a + h = 2a + (2− a) = = 3a 2 − 4a + 4.

Musimy znaleźć minimum funkcji 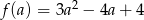2 f (a) = 3a − 4a + 4 na przedziale 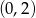(0,2) . Funkcja ta jest parabolą z wierzchołkiem w punkcie

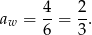
4 2 aw = --= --. 6 3

Zatem najmniejszą długość kwadratu przekątnej otrzymamy dla 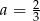2 a = 3 , wartość ta jest równa

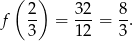
( ) f 2- = 32-= 8. 3 12 3

Długość przekątnej jest równa

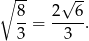
∘ -- √ -- 8- 2--6- 3 = 3 .

Odpowiedź: √ - 2--6 3

Wersja PDF