Zadanie nr 9767045
O ciągu 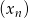 dla
dla 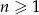 wiadomo, że:
wiadomo, że:
- ciąg
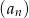 określony wzorem
określony wzorem 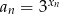 dla
dla 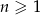 jest geometryczny o ilorazie
jest geometryczny o ilorazie 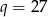 .
. 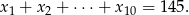
Oblicz 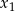 .
.
Rozwiązanie
Po pierwsze zauważmy, że z podanych informacji wynika, że ciąg 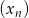 jest arytmetyczny. Rzeczywiście, wiemy, że dla każdego
jest arytmetyczny. Rzeczywiście, wiemy, że dla każdego 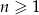 mamy
mamy
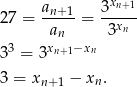
Zatem 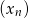 jest ciągiem arytmetycznym o różnicy
jest ciągiem arytmetycznym o różnicy 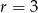 .
.
Korzystając ze wzoru na sumę kolejnych wyrazów ciągu arytmetycznego mamy więc
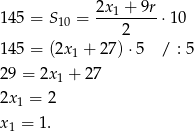
Odpowiedź: