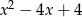/Szkoła średnia/Funkcje - wykresy/Parabola

Zadanie nr 6889554

Napisz wzór funkcji kwadratowej w postaci ogólnej wiedząc, że funkcja ma jedno miejsce zerowe oraz do jej wykresu należą punkty 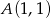A (1,1) oraz B (2,0) .

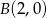Rozwiązanie

Sposób I

Najłatwiej jest skorzystać z postaci kanonicznej. Funkcja kwadratowa, która ma jeden pierwiastek jest postaci 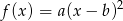f (x) = a(x − b)2 . Współczyniki i 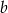wyznaczamy podstawiając podane punkty.

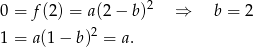
0 = f(2) = a(2− b)2 ⇒ b = 2 1 = a(1 − b)2 = a.

Zatem

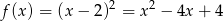
f(x) = (x − 2)2 = x2 − 4x + 4

Sposób II

Jeżeli nie chcemy korzystać z postaci kanonicznej, to szukamy funkcji postaci 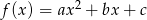f (x) = ax2 + bx + c . Podane punkty dają nam warunki

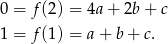
0 = f(2) = 4a + 2b + c 1 = f(1) = a + b + c.

Ponadto informacja o jednym miejscu zerowym oznacza, że

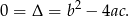
2 0 = Δ = b − 4ac.

Odejmując dwa poprzednie równania stronami mamy

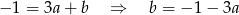
− 1 = 3a+ b ⇒ b = − 1 − 3a

Zatem

c = 1 − a− b = 1 − a + 1 + 3a = 2a + 2 .

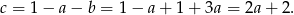
Zatem warunek z 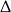-ą daje nam

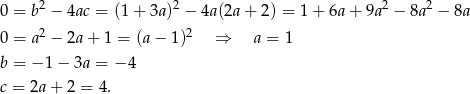
0 = b2 − 4ac = (1 + 3a )2 − 4a (2a+ 2) = 1+ 6a + 9a2 − 8a2 − 8a 2 2 0 = a − 2a + 1 = (a − 1) ⇒ a = 1 b = − 1 − 3a = − 4 c = 2a + 2 = 4.

Odpowiedź: 2 x − 4x + 4

Rozwiązanie Losuj ponownie