/Szkoła średnia/Ciągi/Arytmetyczny/W geometrii/Trójkąt

Zadanie nr 9741785

Dodaj do ulubionych
Dodaj do rozwiązanych

Długości boków trójkąta tworzą trzy kolejne wyrazy ciągu arytmetycznego o różnicy 1. Oblicz długości boków tego trójkąta, jeśli jego pole wynosi 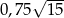√ --- 0,75 15 .

Rozwiązanie

Ze wzoru Herona pole trójkąta o bokach 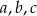a,b,c wyraża się wzorem

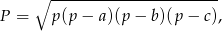
∘ ----------------------- P = p(p − a)(p − b )(p − c),

gdzie 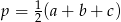p = 1(a+ b+ c) 2 jest połową obwodu. W naszym zadaniu boki trójkąta są postaci 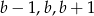b− 1,b,b+ 1 , czyli

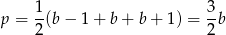
1 3 p = 2-(b− 1+ b+ b + 1) = 2b

i wzór Herona przyjmuje postać

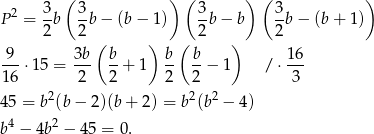
( ) ( ) ( ) 2 3- 3- 3- 3- P = 2b 2b − (b − 1) 2 b− b 2b − (b + 1) ( ) ( ) -9-⋅ 15 = 3b- b-+ 1 b- b-− 1 / ⋅ 1-6 1 6 2 2 2 2 3 2 2 2 45 = b (b− 2)(b+ 2) = b (b − 4) b4 − 4b2 − 45 = 0 .

Równanie jest dwukwadratowe, więc podstawiamy 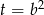t = b2 .

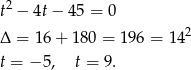
t2 − 4t − 45 = 0 Δ = 16+ 180 = 19 6 = 142 t = − 5, t = 9.

Ujemne rozwiązanie odrzucamy (bo 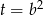2 t = b ) i mamy b = 3 .  
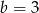Odpowiedź: 2,3,4

Wersja PDF
Rozwiązanie Losuj ponownie