Zadanie nr 9690133

Wykaż, że prawdziwa jest równość 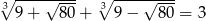3∘ ----√---- ∘3 ----√---- 9 + 80 + 9− 80 = 3 .

Rozwiązanie

Sposób I

Oznaczmy

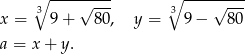
3∘ ----√---- ∘3----√---- x = 9 + 80, y = 9 − 80 a = x+ y.

Korzystając ze wzoru

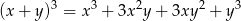
3 3 2 2 3 (x + y ) = x + 3x y + 3xy + y

obliczymy 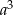. Zanim to jednak zrobimy zauważmy, że

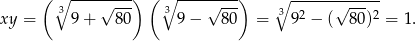
( ∘ ----√----) (∘ ----√---) ∘ ------√------ xy = 39 + 80 3 9− 80 = 39 2 − ( 80 )2 = 1.

Liczymy :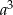

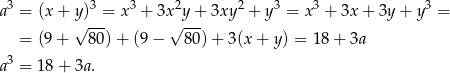
3 3 3 2 2 3 3 3 a = (x + y√ )-= x + 3x√ y-+ 3xy + y = x + 3x + 3y + y = = (9 + 80 )+ (9 − 80 )+ 3 (x+ y) = 18 + 3a 3 a = 1 8+ 3a .

Widzimy zatem, że liczba jest pierwiastkiem wielomianu

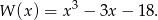
3 W (x ) = x − 3x − 18.

Łatwo sprawdzić, że 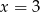x = 3 jest pierwiastkiem tego wielomianu. Aby sprawdzić czy są też inne pierwiastki dzielimy ten wielomian przez (x − 3) .

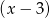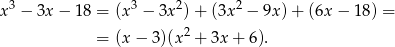
3 3 2 2 x − 3x − 18 = (x − 3x )+ (3x − 9x) + (6x − 18) = = (x− 3)(x2 + 3x + 6).

Ponieważ czynnik kwadratowy nie ma pierwiastków (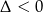 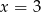Δ < 0 ), x = 3 jest jedynym pierwiastkiem rzeczywistym 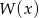W (x) . Zatem a = 3 .

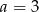Sposób II

Tym razem zwiniemy wyrażenia pod pierwiastkami do pełnych sześcianów.

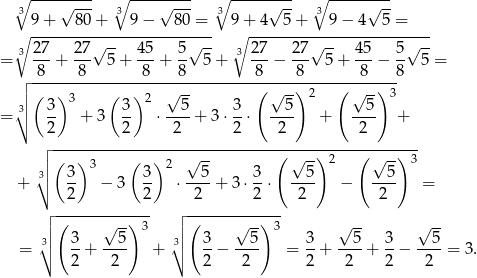
∘3 ----√---- 3∘ ----√---- 3∘ -----√--- ∘3-----√--- 9+ 80+ 9 − 80 = 9+ 4 5 + 9 − 4 5 = ∘ ------------------------- ∘ -------------------------- = 3 27-+ 2-7√ 5 + 45-+ 5√ 5 + 3 27-− 27-√ 5+ 45-− 5-√ 5 = 8 8 8 8 8 8 8 8 ┌│ (--)------(--)----√-----------(-√---)2---(-√---)-3 │∘3 3 3 3 2 5 3 5 5 = -- + 3 -- ⋅----+ 3 ⋅--⋅ ---- + ---- + 2 2 2 2 2 2 ┌│ (--)------(--)----√-----------(-√--)-2---(-√---)3- │∘3 3 3 3 2 5 3 5 5 + 2- − 3 2- ⋅ -2--+ 3 ⋅2-⋅ -2-- − -2-- = ┌│ (-----√---)-3 ┌│ (-----√---)-3 √ -- √ -- │∘3 3- --5- │∘3 3- --5- 3- ---5 3- --5- = 2 + 2 + 2 − 2 = 2 + 2 + 2 − 2 = 3.

Jeżeli komuś podobają się tego typu wzorki, to polecam lekturę poradnika o wzorach Cardano.