Zadanie nr 6517276
Ile zer należy wpisać w miejsce  w zapisie dziesiętnym liczby
w zapisie dziesiętnym liczby 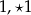 , aby liczba ta była mniejsza niż
, aby liczba ta była mniejsza niż 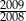 i jednocześnie większa niż
i jednocześnie większa niż 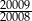 ?
?
A) 1 B) 2 C) 3 D) 4 E) 5
Rozwiązanie
Szukamy liczby naturalnej 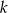 , dla której
, dla której
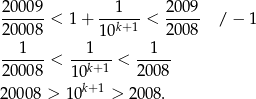
Zatem 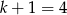 , czyli
, czyli 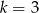 .
.
Odpowiedź: C

