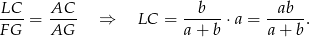Zadanie nr 5321763
Na przyprostokątnych 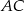 i
i 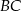 trójkąta prostokątnego
trójkąta prostokątnego 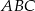 zbudowano, na zewnątrz trójkąta, kwadraty
zbudowano, na zewnątrz trójkąta, kwadraty 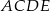 i
i 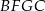 . Odcinek
. Odcinek 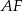 przecina przyprostokątną
przecina przyprostokątną 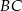 w punkcie
w punkcie 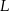 , a odcinek
, a odcinek 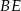 przecina przyprostokątną
przecina przyprostokątną 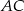 w punkcie
w punkcie 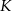 (zobacz rysunek). Udowodnij, że
(zobacz rysunek). Udowodnij, że 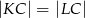 .
.
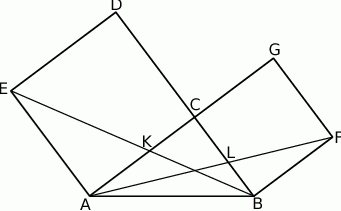
Rozwiązanie
Oznaczmy 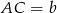 i
i 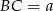 . Zauważmy, że trójkąty
. Zauważmy, że trójkąty 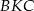 i
i 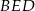 są podobne (bo mają równoległe/pokrywające się boki), więc
są podobne (bo mają równoległe/pokrywające się boki), więc
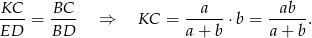
Analogicznie, z podobieństwa trójkątów 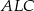 i
i 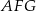 obliczamy długość odcinka
obliczamy długość odcinka 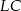 .
.