Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Funkcje/Wielomiany/Różne

Wyszukiwanie zadań

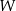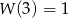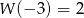Wielomian W jest wielomianem stopnia 5 i spełnia warunki: W (3) = 1 oraz W (−3 ) = 2 . Wykaż, że nie wszystkie współczynniki wielomianu 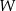W są liczbami całkowitymi.

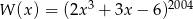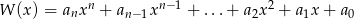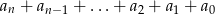Wielomian 3 2004 W (x) = (2x + 3x − 6) , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci W (x) = anxn + an− 1xn−1 + ...+ a2x2 + a1x+ a0 . Oblicz sumę an + a + ...+ a + a + a n− 1 2 1 0 .

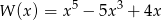Uzasadnij, że dla każdej liczby naturalnej x wartość wielomianu W (x) = x5 − 5x3 + 4x jest liczbą podzielną przez 120.

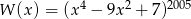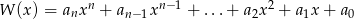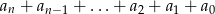Wielomian 4 2 2005 W (x) = (x − 9x + 7) , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci W (x) = anxn + an− 1xn−1 + ...+ a2x2 + a1x+ a0 . Oblicz sumę an + a + ...+ a + a + a n− 1 2 1 0 .