/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Trzywyrazowy

Zadanie nr 5887660

Trzy liczby są kolejnymi wyrazami ciągu geometrycznego, którego iloraz jest różny od 1. Jeżeli weźmiemy kolejno drugą z nich, pierwszą i trzecią, to otrzymamy trzy kolejne wyrazy ciągu arytmetycznego. Jeżeli pierwszy wyraz tego ciągu arytmetycznego zmniejszymy o 7, drugi pozostawimy bez zmian, a trzeci zwiększymy o 3, to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz te liczby.

Wersja PDF

Rozwiązanie

Powiedzmy, że dane liczby to 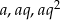2 a,aq,aq , gdzie 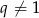q ⁄= 1 . Wiemy, że ciąg 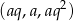(aq,a ,aq 2) jest ciągiem arytmetycznym, a 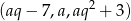(aq − 7 ,a,aq2 + 3) geometrycznym. Daje to nam równania

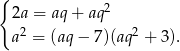
{ 2a = aq+ aq2 2 2 a = (aq− 7)(aq + 3).

Zauważmy, że gdyby 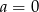a = 0 , to drugie równanie jest sprzeczne, więc możemy założyć, że 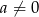a ⁄= 0 . Z pierwszego równania mamy zatem

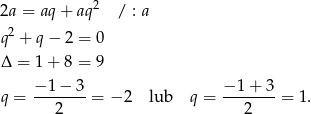
2a = aq + aq2 / : a 2 q + q− 2 = 0 Δ = 1+ 8 = 9 − 1 − 3 − 1 + 3 q = ------- = − 2 lub q = ------- = 1 . 2 2

Z założenia 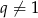q ⁄= 1 , więc 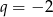q = − 2 . Z drugiego równania układu obliczamy teraz a .

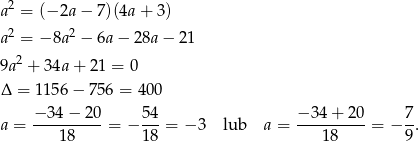
2 a = (−2a − 7)(4a+ 3) a2 = −8a 2 − 6a − 28a− 21 2 9a + 34a + 21 = 0 Δ = 115 6− 7 56 = 400 a = −-34−--20-= − 54-= − 3 lub a = −-34+--20-= − 7. 18 18 18 9

Otrzymujemy więc dwa ciągi spełniające warunki zadania.

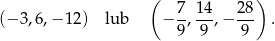
( ) 7- 14- 28- (− 3,6,− 12) lub − 9 , 9 ,− 9 .

 
Odpowiedź: 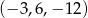(− 3,6,− 12) lub ( 7 14 28) − 9, 9 ,− 9

Wersja PDF