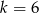Zadanie nr 8898417
Ciąg 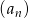 , gdzie
, gdzie 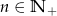 , jest nieskończonym ciągiem arytmetycznym o różnicy 2, w którym pierwszy wyraz jest równy
, jest nieskończonym ciągiem arytmetycznym o różnicy 2, w którym pierwszy wyraz jest równy 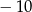 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 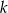 , dla których trzywyrazowy ciąg
, dla których trzywyrazowy ciąg 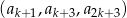 jest ciągiem geometrycznym.
jest ciągiem geometrycznym.
Rozwiązanie
Ze wzoru na  –ty wyraz ciągu arytmetycznego mamy
–ty wyraz ciągu arytmetycznego mamy
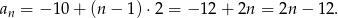
Trzy liczby są kolejnymi wyrazami ciągu geometrycznego jeżeli kwadrat środkowej jest iloczynem dwóch sąsiednich. Mamy więc równanie
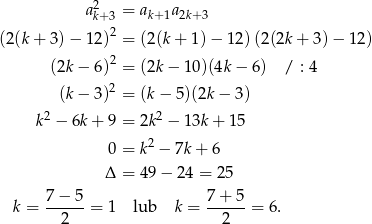
Odpowiedź: 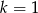 lub
lub