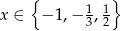/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą/Przez stopnia 1

Zadanie nr 3132583

Reszta z dzielenia wielomianu 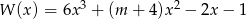3 2 W (x) = 6x + (m + 4)x − 2x − 1 przez dwumian 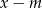x− m jest równa 8. Oblicz wartość 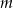m oraz pierwiastki tego wielomianu.

Wersja PDF

Rozwiązanie

Reszta z dzielenia wielomianu 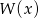W (x) przez dwumian 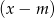(x − m ) to po prostu 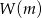W (m) . Mamy więc równanie

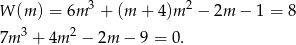
3 2 W (m ) = 6m + (m + 4)m − 2m − 1 = 8 7m 3 + 4m 2 − 2m − 9 = 0.

Aby znaleźć pierwiastki powyższego równania szukamy najpierw pierwiastków wśród dzielników wyrazu wolnego – łatwo zauważyć, że jednym z pierwiastków jest 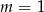m = 1 . Dzielimy teraz lewą stronę równania przez 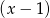(x − 1) – my zrobimy to grupując wyrazy.

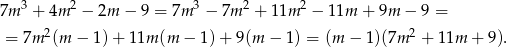
7m 3 + 4m 2 − 2m − 9 = 7m 3 − 7m 2 + 11m 2 − 11m + 9m − 9 = 2 2 = 7m (m − 1) + 11m (m − 1)+ 9(m − 1) = (m − 1)(7m + 11m + 9).

Trójmian w ostatnim nawiasie nie ma pierwiastków (bo 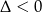Δ < 0 ), więc mamy 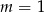m = 1 i wielomian 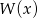W (x) przyjmuje postać

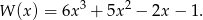
3 2 W (x ) = 6x + 5x − 2x − 1.

Tym razem sprawdzamy, że jednym z jego pierwiastków jest 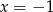x = − 1 . Dzielimy 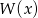W (x ) przez (x+ 1) .

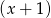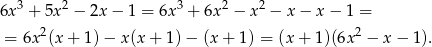
3 2 3 2 2 6x + 5x − 2x − 1 = 6x + 6x − x − x− x− 1 = = 6x2(x + 1) − x(x + 1) − (x + 1) = (x + 1)(6x2 − x− 1).

Rozkładamy jeszcze trójmian w ostatnim nawiasie.

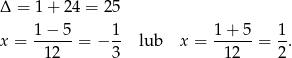
Δ = 1+ 24 = 25 1−--5- 1- 1-+-5- 1- x = 12 = − 3 lub x = 12 = 2.

 
Odpowiedź: 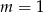m = 1 , { } x ∈ − 1,− 1, 1 3 2

Wersja PDF