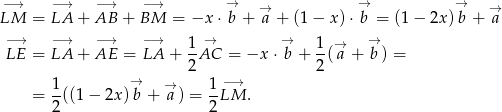Zadanie nr 2483828
Na bokach 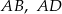 i
i 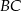 rombu
rombu 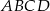 wybrano odpowiednio punkty
wybrano odpowiednio punkty 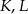 i
i 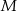 w ten sposób, że odcinki
w ten sposób, że odcinki 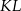 i
i 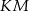 są równoległe do przekątnych rombu. Wykaż, że odcinek
są równoległe do przekątnych rombu. Wykaż, że odcinek 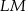 przechodzi przez punkt przecięcia przekątnych rombu.
przechodzi przez punkt przecięcia przekątnych rombu.
Rozwiązanie
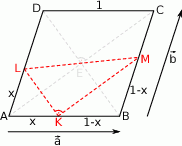
Rozpoczynamy oczywiście od rysunku.
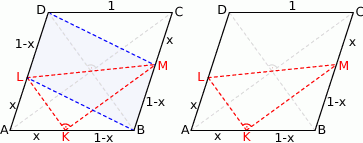
Zauważmy, że trójkąty 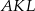 i
i 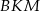 są podobne odpowiednio do
są podobne odpowiednio do 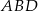 i
i 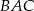 , czyli są równoramienne. Możemy założyć, że bok rombu ma długość 1 oraz oznaczmy
, czyli są równoramienne. Możemy założyć, że bok rombu ma długość 1 oraz oznaczmy 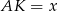 . Wtedy
. Wtedy
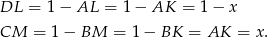
Sposób I
Dorysujmy odcinki 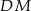 i
i 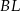 . Odcinki
. Odcinki 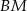 i
i 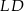 są równoległe oraz mają tę samą długość. Czworokąt
są równoległe oraz mają tę samą długość. Czworokąt 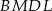 jest więc równoległobokiem. W takim razie jego przekątne
jest więc równoległobokiem. W takim razie jego przekątne 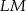 i
i 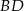 dzielą się na połowy. To z kolei oznacza, że odcinek
dzielą się na połowy. To z kolei oznacza, że odcinek 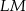 przechodzi przez środek odcinka
przechodzi przez środek odcinka 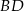 , czyli przez punkt przecięcia przekątnych rombu
, czyli przez punkt przecięcia przekątnych rombu 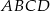 .
.
Sposób II
Niech 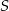 będzie symetrią środkową względem punktu przecięcia przekątnych rombu. Symetria
będzie symetrią środkową względem punktu przecięcia przekątnych rombu. Symetria 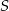 przeprowadza punkty
przeprowadza punkty 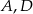 na
na 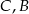 i vice versa. Warunek
i vice versa. Warunek 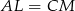 oznacza, że symetria
oznacza, że symetria 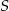 przeprowadza punkt
przeprowadza punkt 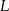 na
na 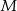 . To jednak oznacza, że środek symetrii
. To jednak oznacza, że środek symetrii 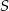 , czyli punkt przecięcia przekątnych rombu jest środkiem odcinka
, czyli punkt przecięcia przekątnych rombu jest środkiem odcinka 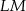 .
.
Sposób III
Niech 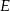 będzie punktem przecięcia przekątnych rombu.
będzie punktem przecięcia przekątnych rombu.
Aby wykazać, że punkt 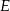 leży na odcinku
leży na odcinku 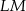 wystarczy wykazać, że wektory
wystarczy wykazać, że wektory 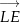 i
i 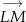 są równoległe. Oznaczmy
są równoległe. Oznaczmy 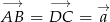 i
i 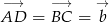 . Mamy więc
. Mamy więc