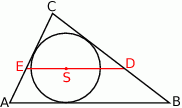
Przez środek 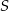 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 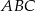 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 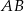 , która przecina boki
, która przecina boki 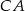 i
i 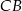 odpowiednio w punktach
odpowiednio w punktach 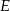 i
i  .
.
Wykaż, że 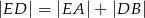 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Przez środek 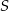 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 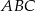 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 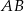 , która przecina boki
, która przecina boki 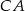 i
i 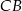 odpowiednio w punktach
odpowiednio w punktach 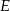 i
i 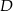 .
.
Wykaż, że 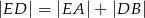 .
.

Okrąg wpisany w trójkąt 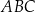 jest styczny do boków
jest styczny do boków 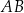 i
i 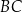 w punktach
w punktach 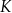 i
i 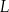 odpowiednio. Na bokach
odpowiednio. Na bokach 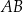 i
i 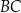 tego trójkąta wybrano punkty
tego trójkąta wybrano punkty 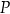 i
i 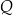 w ten sposób, że odcinek
w ten sposób, że odcinek 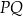 jest styczny do okręgu wpisanego w trójkąt
jest styczny do okręgu wpisanego w trójkąt 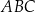 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że jeżeli 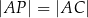 ,
, 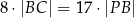 i
i 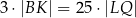 , to trójkąt
, to trójkąt 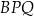 jest rozwartokątny.
jest rozwartokątny.
Kąty w trójkącie mają miary: 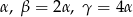 . Wykaż, że długości boków
. Wykaż, że długości boków 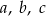 tego trójkąta spełniają równość:
tego trójkąta spełniają równość: 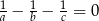 .
.
Okrąg wpisany w trójkąt 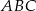 jest styczny do boków
jest styczny do boków 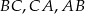 odpowiednio w punktach
odpowiednio w punktach 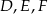 . Punkty
. Punkty 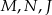 są odpo- wiednio środkami okręgów wpisanych w trójkąty
są odpo- wiednio środkami okręgów wpisanych w trójkąty 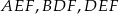 . Dowieść, że punkty
. Dowieść, że punkty 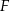 i
i 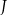 są symetryczne względem prostej
są symetryczne względem prostej 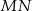 .
.
