/Studia/Analiza/Funkcje/Klasy funkcji/Funkcje cyklometryczne/Wykresy

Zadanie nr 7622441

Naszkicuj wykres funkcji: 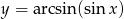y = arcsin(sin x) .

Rozwiązanie

Z deﬁnicji funkcji 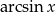arcsinx mamy

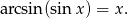
arcsin(sinx ) = x.

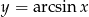Ta równość ma jednak sens tylko dla [ π π] x ∈ − 2, 2- , bo taki jest zbiór wartości y = arcsin x . Spróbujmy teraz zrozumieć co się dzieje dla pozostałych wartości .

Po pierwsze zauważmy, że funkcja ta jest okresowa o okresie 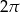– tak jest, bo 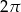2 π jest okresem 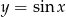y = sin x . Wystarczy zatem narysować kawałek wykresu na przedziale długości 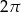, a potem powielić ten kawałek z okresowości. Na razie wiemy co się dzieje na przedziale długości 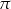, więc sprawdźmy jeszcze co otrzymamy np. dla [ ] x ∈ π-, 3π 2 2 . Mamy wtedy

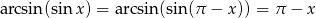
arcsin(sin x) = arcsin(sin(π − x )) = π − x

(bo [ π- π-] π − x ∈ − 2,2 ). Teraz bez trudu rysujemy wykres.

Wersja PDF