/Studia/Liczby zespolone/Interpretacja geometryczna

Zadanie nr 6957152

Dodaj do ulubionych
Dodaj do rozwiązanych

Narysować na płaszczyźnie zespolonej zbiór punktów spełniających warunek 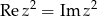Re z2 = Im z2 .

Rozwiązanie

Sposób I

Jeżeli 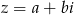z = a + bi , to

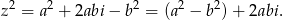
2 2 2 2 2 z = a + 2abi− b = (a − b )+ 2abi.

Podany warunek daje nam więc równanie

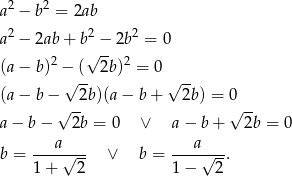
2 2 a − b = 2ab a2 − 2ab + b2 − 2b2 = 0 √ -- (a − b)2 − ( 2b)2 = 0 √ -- √ -- (a − b− √ -2b)(a − b+ 2b) = 0√ -- a − b− 2b = 0 ∨ a− b + 2b = 0 b = ----a√--- ∨ b = ---a√---. 1 + 2 1 − 2

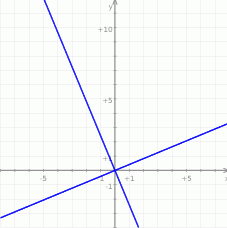
Każda z równości opisuje prostą na płaszczyźnie, w sumie mamy więc dwie proste (które jak łatwo sprawdzić są prostopadłe).

Sposób II

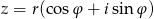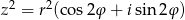Jeżeli z = r(cos φ + isinφ ) , to z2 = r2(cos2 φ + isin2 φ) i mamy równanie

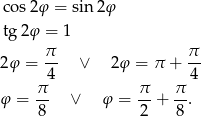
cos2φ = sin2 φ tg 2φ = 1 π π 2φ = -- ∨ 2φ = π + -- 4 4 φ = π- ∨ φ = π-+ π-. 8 2 8

Każdy z warunków opisuje prostą na płaszczyźnie. Łatwo te proste teraz narysować - jedna jest dwusieczną kąta między prostą 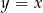y = x i osią 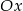Ox , a druga jest do niej prostopadła.

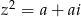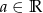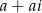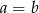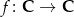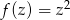Jeszcze na koniec komentarz. Szukaliśmy liczb zespolonych spełniających warunek 2 z = a + ai dla pewnego a ∈ R , czyli otrzymane proste dają wszystkie pierwiastki kwadratowe z liczb postaci a+ ai , lub jak ktoś woli, znaleźliśmy przeciwobraz prostej a = b przy odwzorowaniu f : C → C , f (z) = z2 .

PIC

Wersja PDF
Rozwiązanie Losuj ponownie