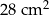/Szkoła podstawowa/Geometria

Zadanie nr 2400932

Dodaj do ulubionych
Dodaj do rozwiązanych

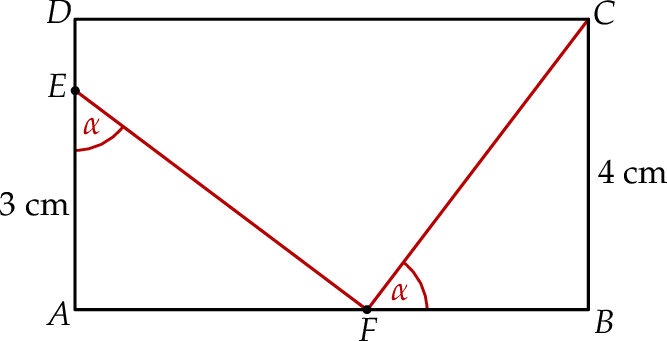
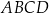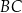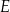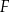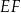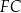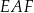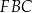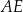Na rysunku przedstawiono prostokąt ABCD , w którym bok BC ma długość 4 cm. Na bokach prostokąta zaznaczono punkty E i F oraz narysowano odcinki EF i F C tak, że powstały dwa jednakowe trójkąty EAF i FBC . W obu trójkątach zaznaczono kąty o takiej samej mierze α . Odcinek AE ma długość 3 cm.

ZINFO-FIGURE

Oblicz pole prostokąta 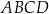ABCD .

Rozwiązanie

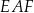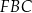Wiemy, że trójkąty EAF i F BC są przystające (takie same), więc

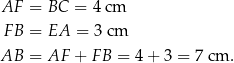
AF = BC = 4 cm F B = EA = 3 cm AB = AF + F B = 4 + 3 = 7 cm .

Pole prostokąta 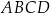ABCD jest więc równe

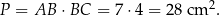
P = AB ⋅BC = 7⋅4 = 28 cm 2.

 
Odpowiedź: 28 cm 2

Wersja PDF