Zadanie nr 8920065
Wiedząc, że wektory 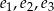 są liniowo niezależne sprawdź liniową niezależność wektorów
są liniowo niezależne sprawdź liniową niezależność wektorów 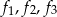 jeżeli
jeżeli 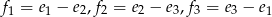 .
.
Rozwiązanie
Ponieważ
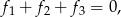
więc wektory są linowo zależne.
Odpowiedź: Wektory są linowo zależne.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wiedząc, że wektory 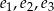 są liniowo niezależne sprawdź liniową niezależność wektorów
są liniowo niezależne sprawdź liniową niezależność wektorów 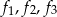 jeżeli
jeżeli 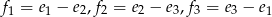 .
.
Ponieważ
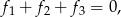
więc wektory są linowo zależne.
Odpowiedź: Wektory są linowo zależne.
