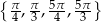Zadanie nr 3927746

Rozwiąż równanie 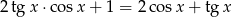2tg x⋅ cosx + 1 = 2cos x+ tg x w przedziale ⟨0,2π ⟩ .

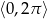Rozwiązanie

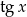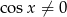Oczywiście ze względu na tg x , musi być co sx ⁄= 0 .

Sposób I

Przekształcamy równanie – przenosimy wszystko na jedną stronę i próbujemy coś wyłączyć przed nawias.

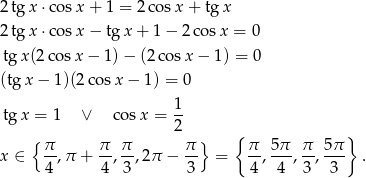
2tg x ⋅cosx + 1 = 2co sx + tgx 2tg x ⋅cosx − tg x + 1− 2co sx = 0 tg x(2c osx − 1) − (2 cosx − 1) = 0 (tgx − 1 )(2 cos x− 1) = 0 1 tg x = 1 ∨ co sx = -- { 2 } { } x ∈ π-,π + π-, π,2 π − π- = π-, 5π-, π-, 5π . 4 4 3 3 4 4 3 3

Sposób II

Tym razem przekształcimy równanie pozbywając się tangensa.

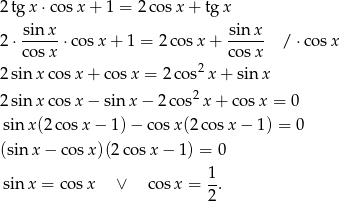
2tg x⋅ cosx + 1 = 2cos x+ tg x 2⋅ sinx-⋅co sx + 1 = 2 cos x+ sinx- / ⋅co sx cosx cosx 2sin xco sx + cos x = 2 cos2x + sinx 2sin xco sx − sinx − 2 cos2x + c osx = 0 sinx (2co sx − 1)− cosx (2cos x − 1) = 0 (sin x − cos x)(2 cosx − 1) = 0 1 sinx = cos x ∨ cos x = --. 2

Z drugiego równania mamy

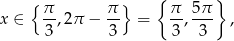
{ π π} { π 5π } x ∈ --,2π − -- = --,--- , 3 3 3 3

a pierwsze równanie przekształcamy następująco

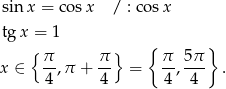
sin x = cosx / : cos x tgx = 1 {π π } { π 5π } x ∈ --,π + -- = --,--- . 4 4 4 4

Odpowiedź: { } π4-, π3, 5π4-, 5π3