Zadanie nr 6144252
Macierz 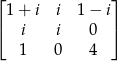 przedstawić w postaci sumy dwóch macierzy, z których jedna jest hermitowska a druga antyhermitowska.
przedstawić w postaci sumy dwóch macierzy, z których jedna jest hermitowska a druga antyhermitowska.
Rozwiązanie
Niech 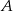 będzie macierzą hermitowską, a
będzie macierzą hermitowską, a 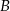 antyhermitowską oraz
antyhermitowską oraz
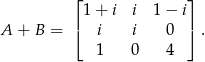
Wiemy, że 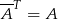 i
i 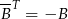 . Zatem sprzęgając hermitowsko powyższą równość mamy
. Zatem sprzęgając hermitowsko powyższą równość mamy
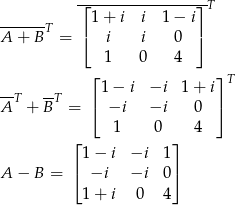
Dodajemy teraz do tej równości równość z samego początku
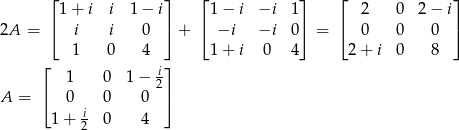
Zatem
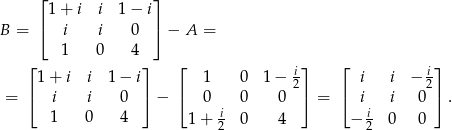
Oczywiście powyższa procedura działa dla dowolnej macierzy 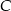 i daje rozkład
i daje rozkład
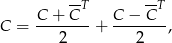
gdzie pierwsza macierz jest hermitowska, a druga antyhermitowska.

