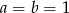Zadanie nr 7420022
Dla jakich wartości parametrów  i
i 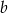 rząd macierzy
rząd macierzy 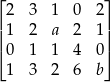 jest najmniejszy?
jest najmniejszy?
Rozwiązanie
Liczymy rząd i nie przejmujemy się parametrami (choć staramy się ich unikać przy odejmowaniach).
![⌊ ⌋ ⌊ ⌋ 2 3 1 0 2 2 3 − 2 −1 2 2 rk ||1 2 a 2 1 || = rk || 1 2 a− 2 − 6 1|| = ⌈0 1 1 4 0 ⌉ ⌈ 0 1 0 0 0⌉ 1 3 2 6 b K3−K 2 1 3 − 1 − 6 b K4−4K 2 ⌊2 − 2 − 12 2 ⌋ ⌊ 2 0 0 0 ⌋ ⌈ ⌉ ⌈ ⌉ = rk 1 a − 2 − 6 1 K +K + 1 = rk 1 a− 1 0 0 + 1 = 1 − 1 − 6 b K32+ 6K11 1 0 0 b− 1 K4−K1 [a − 1 0 ] = rk + 2. 0 b − 1](https://img.zadania.info/zad/7420022/HzadR0x.gif)
Widać więc, że najmniejszy rząd otrzymamy dla 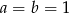 . Wynosi on wtedy 2.
. Wynosi on wtedy 2.
Odpowiedź: