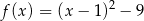/Szkoła średnia/Funkcje - wykresy/Parabola/Wzór z wykresu/3 niewiadome

Zadanie nr 5682794

Znajdź wzór funkcji kwadratowej 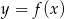y = f (x) , której wykresem jest parabola o wierzchołku 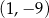(1 ,−9 ) przechodząca przez punkt o współrzędnych 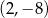(2,− 8) . Otrzymaną funkcję przedstaw w postaci kanonicznej. Oblicz jej miejsca zerowe i naszkicuj wykres.

Wersja PDF

Rozwiązanie

Korzystamy ze wzoru na postać kanoniczną funkcji kwadratowej

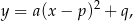
2 y = a(x − p ) + q ,

gdzie 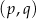(p,q) –współrzędne wierzchołka paraboli. Z danych zadania wiemy, że 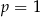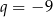p = 1 , q = − 9 . Mamy zatem:

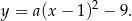
y = a(x − 1 )2 − 9.

Wiemy ponadto, że punkt 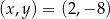(x,y) = (2,− 8) należy do wykresy tej funkcji, co daje nam równanie:

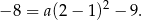
− 8 = a(2 − 1)2 − 9.

Łatwo stąd wyliczyć, że 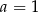a = 1 , czyli wzór funkcji w postaci kanonicznej:

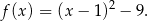
2 f(x) = (x − 1) − 9 .

Aby znaleźć miejsca zerowe, korzystamy ze wzoru 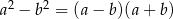2 2 a − b = (a − b)(a + b) :

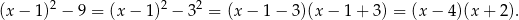
2 2 2 (x − 1) − 9 = (x − 1 ) − 3 = (x− 1− 3)(x− 1+ 3) = (x − 4)(x + 2).

Otrzymujemy stąd miejsca zerowe: 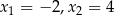x1 = − 2,x2 = 4 . Oczywiście zamiast stosować wzór skróconego mnożenia mogliśmy skorzystać ze wzoru na pierwiatki z Δ .

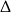Mając wierzchołek i miejsca zerowe łatwo narysować wykres.

PIC

 
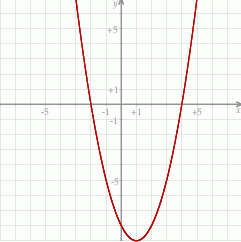
Odpowiedź: f (x) = (x − 1)2 − 9

Wersja PDF