Zadanie nr 9230161
W pudełku znajduje się 8 piłeczek oznaczonych kolejnymi liczbami naturalnymi od 1 do 8. Losujemy jedną piłeczkę, zapisujemy liczbę na niej występującą, a następnie zwracamy piłeczkę do urny. Tę procedurę wykonujemy jeszcze dwa razy i tym samym otrzymujemy zapisane trzy liczby. Oblicz prawdopodobieństwo wylosowania takich piłeczek, że iloczyn trzech zapisanych liczb jest podzielny przez 4. Wynik podaj w postaci ułamka zwykłego.
Rozwiązanie
Wszystkich trzyelementowych ciągów 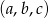 o wyrazach ze zbioru
o wyrazach ze zbioru 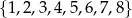 jest
jest
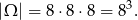
Sposób I
Jeżeli się chwile zastanowimy, to powinno stać się jasne, że jest dość dużo zdarzeń sprzyjających, więc zamiast zajmować się zdarzeniem opisanym w treści zadania, zajmijmy się zdarzeniem przeciwnym, gdy iloczyn otrzymanych trzech liczb nie dzieli się przez 4.
Są dwa rodzaje takich zdarzeń: albo wylosowaliśmy same liczby nieparzyste, albo wylosowaliśmy dokładnie jedną dwójkę lub dokładnie jedną szóstkę. Zdarzeń pierwszego rodzaju jest
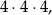
a zdarzeń drugiego rodzaju jest
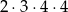
(na 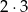 sposoby wybieramy dwójkę lub szóstkę oraz miejsce tej liczby, a potem na
sposoby wybieramy dwójkę lub szóstkę oraz miejsce tej liczby, a potem na 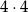 sposoby umieszczamy na pozostałych miejscach dwie liczby nieparzyste).
sposoby umieszczamy na pozostałych miejscach dwie liczby nieparzyste).
Interesujące nas prawdopodobieństwo jest więc równe
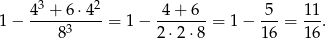
Sposób II
Tym razem liczymy wprost.
Są 4 liczby spełniające warunki zadania, w których wszystkie otrzymane wyniki są takie same:
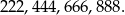
Liczb z dokładnie dwoma równymi cyframi parzystymi (tzn. takich jak 122, 424 itp.) jest
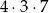
(na 4 sposoby wybieramy powtarzającą się cyfrę parzystą, na 3 sposoby miejsce dla trzeciej cyfry i na 7 sposobów tę trzecią cyfrę).
Liczb z dokładnie dwoma cyframi nieparzystymi (tzn. np. 411, 585 itp.) jest
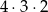
(na 4 sposoby wybieramy powtarzającą się cyfrę nieparzystą, na 3 sposoby miejsce dla trzeciej cyfry i na 2 sposoby tę trzecią cyfrę – musi to być 4 lub 8).
Pozostało zająć się liczbami o trzech różnych cyfrach. Jest
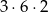
liczb, których dwoma cyframi są 4 i 8 (na 3 sposoby wybieramy miejsce dla trzeciej cyfry, na 6 sposobów wybieramy tę cyfrę oraz na 2 sposoby możemy umieścić 4 i 8).
Jeżeli dokładnie jedną z tych cyfr jest 4 lub 8, to jest
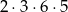
takich liczb (wybieramy 4 lub 8, potem na 3 sposoby wybieramy gdzie ta cyfra ma być umieszczona, potem dobieramy bez powtórzeń pozostałe dwie cyfry).
Ostatnia możliwość, to gdy dwie z cyfr to 2 i 6, a trzecia jest nieparzysta. Takich liczb jest
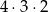
(na 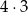 sposoby wybieramy cyfrę nieparzystą oraz jej miejsce, potem na dwa sposoby możemy umieścić 2 i 6).
sposoby wybieramy cyfrę nieparzystą oraz jej miejsce, potem na dwa sposoby możemy umieścić 2 i 6).
Interesujące nas prawdopodobieństwo jest więc równe
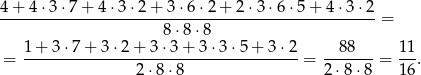
Odpowiedź: