Zadanie nr 4895662
Oblicz, ile jest wszystkich siedmiocyfrowych liczb naturalnych, w których zapisie dziesiętnym występują dokładnie trzy cyfry 1 i dokładnie dwie cyfry 2.
Rozwiązanie
Jak zwykle w zadaniach z cyframi musimy uważać na pierwszą cyfrę – żeby przypadkiem nie umieścić tam zera. Z tego powodu rachunek, ile jest liczb spełniających warunki zadania rozbijemy na trzy przypadki.
Załóżmy najpierw, że pierwsza cyfra (najbardziej znacząca) nie jest jedynką ani dwójką. W takiej sytuacji miejsca dla jedynek możemy wybrać na
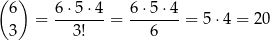
sposobów. Potem wybieramy miejsca dla dwójek – możemy to zrobić na
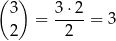
sposoby. Następnie wybieramy pierwszą cyfrę – możemy to zrobić na 7 sposobów (nie może być zerem, jedynką ani dwójką). Na koniec ostatnią z nieustalonych cyfr wybieramy na 8 sposobów (nie może być jedynka ani dwójka). W tym przypadku jest więc
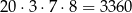
liczb spełniających warunki zdania.
Jeżeli teraz pierwszą cyfrą tworzonej liczby jest jedynka, to miejsca dla pozostałych dwóch jedynek możemy wybrać na
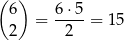
sposobów. Potem na
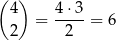
sposobów wybieramy miejsca dla dwójek. Na koniec na każdym z pozostałych dwóch miejsc umieszczamy jedną z 8 cyfr. W tym przypadku jest więc
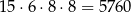
liczb spełniających warunki zdania.
Jeżeli wreszcie na pierwszym miejscu umieścimy dwójkę, to na 6 sposób wybieramy miejsce dla drugiej dwójki. Na
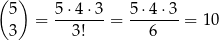
sposobów wybieramy miejsce dla jedynek i na koniec na każdym z pozostałych dwóch miejsc umieszczamy jedną z 8 cyfr. W tym przypadku jest więc
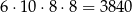
liczb spełniających warunki zdania.
W sumie jest więc
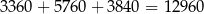
takich liczb.
Odpowiedź: 12960

