/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 7484789

Oblicz, ile jest liczb naturalnych trzycyfrowych podzielnych przez 6 lub podzielnych przez 15.

Wersja PDF

Rozwiązanie

Obliczmy najpierw ile jest liczb trzycyfrowych podzielnych przez 6. Liczby te to

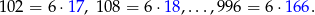
1 02 = 6 ⋅17, 108 = 6 ⋅18,...,996 = 6⋅ 166.

Widać, że liczby te tworzą ciąg arytmetyczny długości 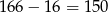166− 16 = 15 0 .

Teraz obliczmy ile jest liczb trzycyfrowych podzielnych przez 15. Liczby te to

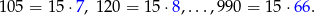
1 05 = 15 ⋅7, 120 = 15 ⋅8,...,990 = 15⋅ 66.

Liczby te tworzą ciąg arytmetyczny długości 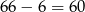66 − 6 = 60 .

W sumie jest więc 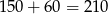150+ 60 = 210 liczb podzielnych przez 6 lub 15.

Jest jednak mały kłopot, bo liczby, które dzielą się jednocześnie przez 6 i przez 15, czyli takie, które dzielą się przez 30, policzyliśmy podwójnie. Sprawdźmy ile ich jest. Liczby trzycyfrowe podzielne przez 30 to

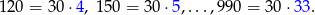
1 20 = 30 ⋅4, 150 = 30 ⋅5,...,990 = 30⋅ 33.

Widać, że jest ich 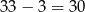33 − 3 = 3 0 . Musimy tę liczbę odjąć od wcześniej otrzymanej sumy (bo liczyliśmy te liczby dwa razy). Daje nam to

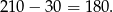
210 − 30 = 180.

 
Odpowiedź: 180

Wersja PDF