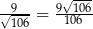Zadanie nr 9878305
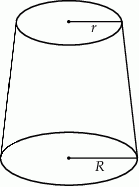
Objętość stożka ściętego (przedstawionego na rysunku) można obliczyć ze wzoru 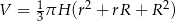 , gdzie
, gdzie  i
i 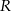 są promieniami podstaw (
są promieniami podstaw (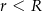 ), a
), a 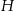 jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa 10, objętość
jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa 10, objętość 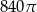 , a
, a 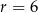 . Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw.
. Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw.
Rozwiązanie
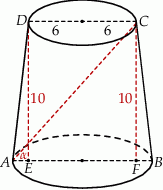
Przekrojem ściętego stożka jest trapez równoramienny  .
.
Obliczmy najpierw promień większej podstawy – korzystamy z podanej objętości.
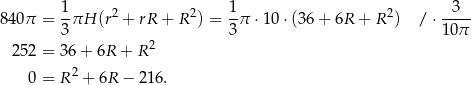
Rozwiązujemy otrzymane równanie kwadratowe.
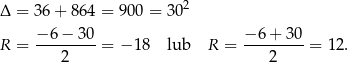
Ujemne rozwiązanie odrzucamy i mamy 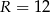 . Patrzymy teraz na trapez równoramienny
. Patrzymy teraz na trapez równoramienny 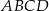 i jego wysokości
i jego wysokości 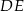 i
i 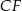 .
.
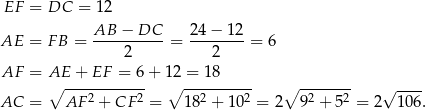
Stąd
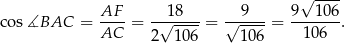
Odpowiedź: