Zadanie nr 3126384
Określić wymiary otwartego zbiornika prostopadłościennego o objętości 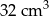 tak, aby jego pole powierzchni było minimalne.
tak, aby jego pole powierzchni było minimalne.
Rozwiązanie
Zacznijmy od rysunku.
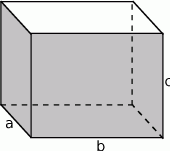
Powierzchnia wanny wyraża się wzorem
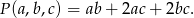
Chcemy znaleźć minimum tej funkcji przy warunku 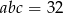 i
i 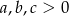 .
.
Sposób I
Z podanego warunku możemy sytuację sprowadzić do funkcji dwóch zmiennych.
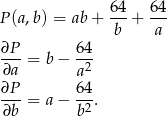
Rozwiązujemy teraz układ równań 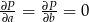 . Z pierwszego równania mamy
. Z pierwszego równania mamy 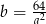 . Wstawiamy to do drugiego i mamy
. Wstawiamy to do drugiego i mamy
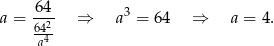
Stąd 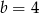 . Sprawdzamy teraz określoność drugiej pochodnej.
. Sprawdzamy teraz określoność drugiej pochodnej.
![[ ] 1283 1 d 2P(a,b) = a 128 1 b3 [2 1] d 2P(4,4) = . 1 2](https://img.zadania.info/zad/3126384/HzadR9x.gif)
Ponieważ druga pochodna jest dodatnio określona, w punkcie 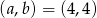 mamy minimum lokalne. Pozostał nam trudny problem ustalenia, czy jest to minimum globalne.
mamy minimum lokalne. Pozostał nam trudny problem ustalenia, czy jest to minimum globalne.
Jeżeli 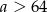 i
i 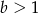 to
to 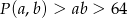 Jeżeli natomiast
Jeżeli natomiast 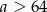 i
i 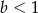 to
to 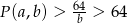 . Możemy zatem założyć
. Możemy zatem założyć 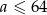 . Podobnie, możemy założyć, że
. Podobnie, możemy założyć, że 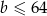 . Ponadto uzasadniamy, że można założyć
. Ponadto uzasadniamy, że można założyć ![a,b ∈ [1,64] × [1,64]](https://img.zadania.info/zad/3126384/HzadR19x.gif) . Teraz mamy już funkcję na zwartym kwadracie i wiemy, że przyjmuje ona na tym zbiorze minimum globalne. Jest ono przyjmowane albo we wcześniej znalezionym minimum lokalnym, albo na brzegu. Punkty brzegu łatwo jednak wyeliminować wstawiając do wzoru na
. Teraz mamy już funkcję na zwartym kwadracie i wiemy, że przyjmuje ona na tym zbiorze minimum globalne. Jest ono przyjmowane albo we wcześniej znalezionym minimum lokalnym, albo na brzegu. Punkty brzegu łatwo jednak wyeliminować wstawiając do wzoru na 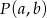 kolejno wartości
kolejno wartości 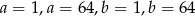 .
.
Sposób II
Najprostsze rozwiązanie uzyskamy stosując nierówność między średnimi. Mamy

W dodatku równość w tej nierówności zachodzi dokładnie wtedy gdy wszystkie trzy liczby są równe, co prowadzi do trójki 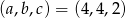 .
.
Sposób III
Stosujemy metodę mnożników Lagrange’a. Na początek sprawdzamy, że funkcja 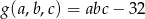 jest nieosobliwa i szukamy minimum funkcji
jest nieosobliwa i szukamy minimum funkcji
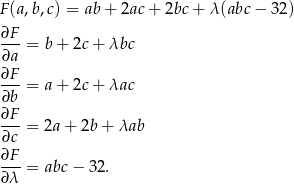
Musimy teraz rozwiązać układ równań 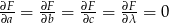 . Z ostatniego równania mamy
. Z ostatniego równania mamy 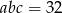 i mnożąc pierwsze trzy równania przez
i mnożąc pierwsze trzy równania przez 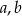 i
i  odpowiednio mamy układ
odpowiednio mamy układ
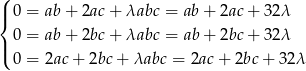
Odejmując od pierwszego równania drugie mamy
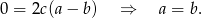
Podobnie, jak od trzeciego odejmiemy drugie, to mamy
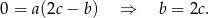
Zatem 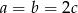 . Z równości
. Z równości 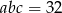 mamy wtedy
mamy wtedy
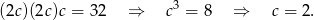
Zatem 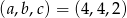 . Pozostało wykazać, że w tym punkcie jest minimum globalne (zbiór, na którym badamy funkcję nie jest zwarty, więc trzeba uważać). Liczymy drugą pochodną funkcji
. Pozostało wykazać, że w tym punkcie jest minimum globalne (zbiór, na którym badamy funkcję nie jest zwarty, więc trzeba uważać). Liczymy drugą pochodną funkcji 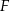 w punkcie
w punkcie 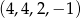 (bo
(bo 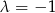 ).
).
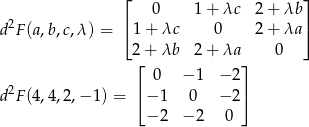
Określoność tej formy badamy przy warunku 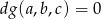 , gdzie
, gdzie 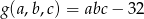 . Mamy
. Mamy
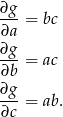
Co daje nam Hesjan obrzeżony
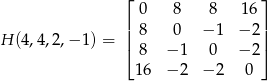
Łatwo sprawdzić, że minory 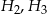 są ujemne, czyli forma jest wszędzie dodatnio określona. Zatem w punkcie
są ujemne, czyli forma jest wszędzie dodatnio określona. Zatem w punkcie 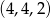 jest lokalne minimum. Globalność tego minimum uzasadniamy podobnie jak w I sposobie. Widać więc, że dla
jest lokalne minimum. Globalność tego minimum uzasadniamy podobnie jak w I sposobie. Widać więc, że dla 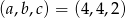 mamy minimum globalne.
mamy minimum globalne.
Odpowiedź: 4 cm,4 cm,2 cm

